Tema 3: Mostreo, intervalos de confianza e contraste de hipóteses
Mostreo
Poboación: conxunto de todos os suxeitos que queremos estudar.
Parámetros poboacionais: \[\mu\], \[\sigma\] e \[p\]
Mostra: subconxunto dos elementos da poboación
Parámetros mostrais ou Estatísticos: \[\overline{X}\], \[S\] e \[\hat{p}\]
Técnicas de mostreo
M. aleatorio simple
Se escogen todos los elementos de la muestra de forma aleatoria.
M. aleatorio sistemático
Se escoge el primer elemento de la muestra de forma aleatoria y despues se va haciendo saltos de tamaño \[c= N/n\]
M. aleatorio estratificado
Se divide la población en estratos y se hace un muestro simple de cada estrato. El número de elementos seleccionado de cada estato es proporcional al número de elementos de cada estrato.
M. aleatorio por conglomerados
Se divide la pobloación en conglomerados, se seleccionan uno o varios conglomerados y despues se hace un muestreo aleatorio simple de cada conglomerado.
Estratos vs Conglomerados
Unha mostra é representativa cando ao estudar un parámetro desta mostra (estatístico) este se acerca ao parámetro da poboación.
Estimación
Os parámetros da mostra axúdannos a inferir os parámetros da poboación.
Tipos de estimación
- Estimación puntual: eliximos un único valor para estimar o parámetro da poboación.
- Estimación por intervalos de confianza: eliximos un intervalo no que estamos "seguros" de que estará o valor do parámetro poblacional que estudamos.
Estimación por intervalos de confianza
Unha fábrica de conservas desexa coñecer o tempo que tarda en botarse a perder un produto que ten almacenado. Elixe unha mostra de 400 unidades, resultando que o tempo medio de descomposición destes produtos é de 172 horas. Por experiencias anteriores coñécese que a desviación típica da variable normal tempo de descomposición é de 5 horas. Cun nivel de confianza do 95%, entre que valores se atopa o tempo medio de descomposición para a totalidade do produto almacenado?
Distribución da media mostral
Teorema central do límite
 Introducción a la estadística y sus aplicaciones. Ricardo Cao Abad et al.
Introducción a la estadística y sus aplicaciones. Ricardo Cao Abad et al.
Media muestral
\[\overline{X} \sim N(\mu, \frac{\sigma}{\sqrt{n}} \]
1Considérese unha poboación na que se estuda unha característica X que segue unha distribución normal de media \[\mu = 12\] e varianza \[\sigma^2 = 16\]. Pídese:
- a Probabilidade de que un elemento da poboación, elixido ó chou, teña a característica superior a 14.
- b Considérase unha mostra aleatoria de tamaño n=9. Cal é a probabilidade de que a media mostral \[\overline{X}\] teña un valor superior a 14?
Intervalo de confianza para a media
EUnha fábrica de conservas desexa coñecer o tempo que tarda en botarse a perder un produto que ten almacenado. Elixe unha mostra de 400 unidades, resultando que o tempo medio de descomposición destes produtos é de 172 horas. Por experiencias anteriores coñécese que a desviación típica da variable normal tempo de descomposición é de 5 horas. Cun nivel de confianza do 95%, entre que valores se atopa o tempo medio de descomposición para a totalidade do produto almacenado?
2Un supervisor someteu unha mostra de 16 fusibles a unha certa sobrecarga. Os tempos que tardaron en fundirse deron unha media de 10,63 minutos. Considerando que a variable “tempo que tarda en fundirse un fusible sometido a esa sobrecarga” é normal cunha desviación típica de 2,48 minutos, construír un intervalo de confianza para a media poboacional cun nivel de confianza do 95%.
3Unha fábrica desexa coñecer o tempo que tarda en estragarse un produto que ten almacenado. Para isto, elixe unha mostra de 100 unidades, resultando un tempo medio de descomposición de 120 horas. Por experiencias anteriores coñécese que a desviación típica da variable normal tempo de descomposición é de 5 horas. Cun nivel de confianza do 95%, ¿entre que valores se atopa o tempo medio de descomposición para a totalidade do produto almacenado?
4Para determina-la idade promedio dos seus clientes, un fabricante de roupa para cabaleiro colle unha mostra aleatoria de 50 clientes e calcula a súa idade media \[ \overline{X} = 36 \] anos. Se se sabe que a variable idade segue unha distribución normal con desviación típica \[ \sigma = 12 \] anos, determinar cun 95% de confianza o intervalo da media de idade de tódolos clientes.
Cálculo da d. típica, o tamaño da mostra, o erro, o nivel de confianza, etc.
5Sábese que o gasto semanal (en euros) en ocio para os mozos dunha certa cidade segue unha distribución normal con desviación típica \[ \sigma \] coñecida.
- a Para unha mostra aleatoria de 100 mozos desa cidade, o intervalo de confianza ó 95% para o gasto medio semanal \[ \mu \] é \[ (27,33) \]. Calcula-la correspondente media mostral e o valor de \[ \sigma \].
- a Que número de mozos teríamos que seleccionar ó chou, como mínimo, para garantir, cunha confianza do 95%, unha estimación de dito gasto medio cun erro máximo non superior a 2 euros semanais?
6 Un deseñador industrial desexa estimar o tempo medio que tarda un adulto en ensamblar un certo tipo de xoguete. Por experiencias previas coñece que a variable tempo de ensamblaxe segue unha distribución normal, con media μ e desviación típica \[ \sigma = 5\] minutos.
- a Seleccionada ao chou unha mostra de 64 adultos a súa media resultou ser de 20 minutos. Entre que valores se atopa o tempo medio real de ensamblaxe, cunha confianza do 95%?
- bSupoñamos que \[ \mu = 20\] minutos. Por razóns comerciais decide que cambiará o modelo de xoguete se o tempo medio de ensamblaxe, en mostras de 64 adultos, é superior a 21 minutos, ¿con que probabilidade tomará esa decisión?
- c Calcula cantos adultos deberá seleccionar, como mínimo, para garantir, cun 95% de confianza, unha estimación de dito tempo medio cun error máximo non superior a un minuto.
7O peso dos alumnos de bacharelato dunha certa cidade ten unha media descoñecida e unha desviación típica kg. Tomamos unha mostra aleatoria de 100 alumnos de bacharelato desa cidade:
- a Se a media da mostra é de 60 kg, calcular cun nivel de confianza do 99%, o intervalo de confianza para o peso medio \[ \mu \] de tódolos alumnos de bacharelato da cidade.
- b Faise a seguinte afirmación: “o peso medio dos alumnos de bacharelato desa cidade está comprendido entre 59 e 61 kg”, con que nivel de confianza se fai esta afirmación?
Distribución da proporción mostral
Teorema central do límite
 Introducción a la estadística y sus aplicaciones. Ricardo Cao Abad et al.
Introducción a la estadística y sus aplicaciones. Ricardo Cao Abad et al.
Proporción mostral
\[\hat{p} \sim N(p, \sqrt{\frac{pq}{n}} \]
Intervalo de confianza para a proporción
8A proporción de mulleres dunha poboación portadoras de hemofilia é descoñecida. Para estimala elíxese unha mostra aleatoria de 500 mulleres entre as que se encontran 80 portadoras da enfermidade.
- aCalcula un intervalo do 95% de confianza para a proporción de mulleres portadoras de hemofilia desa poboación.
- aSupoñendo que aínda non se tomou a mostra e queremos facer a estimación cometendo un erro non superior ao 2%, cun 95% de confianza, de que tamaño debería ser a devandita mostra?
9Nun estanque deséxase estimar a porcentaxe de peixes dourados. Para iso, tómase unha mostra aleatoria de 700 peixes e atópase que exactamente 70 deles son dourados.
- a Acha, cun nivel de confianza do 99%, un intervalo para estimar a proporción de peixes dourados no estanque.
- b No intervalo anterior, canto vale o erro de estimación?
- c Considerando dita mostra, que lle ocorrería ao erro de estimación se aumentase o nivel de confianza? Xustifica a resposta.
10
- a Nunha mostra aleatoria de estudantes \[n=25\] de bacharelato, o 75% afirman querer realizar estudos universitarios. Calcula un intervalo de confianza para a proporción de estudantes de bacharelato que queren realizar estudos universitarios cun nivel de confianza do 90%
- b Se se sabe que 8 de cada 10 estudantes de bacharelato afirman querer realizar estudos universitarios e tomamos unha mostra aleatoria de \[ n=100 \] estudantes, cal é a probabilidade de que a proporción de estudantes da mostra que queren realizar estudos universitarios sexa superior ao 65%?
11
- a Nunha mostra aleatoria de 200 clientes dun centro comercial, 150 efectúan as súas compras utilizando a tarxeta propia do centro. Calcula un intervalo do 95% de confianza para a proporción de clientes que efectúan as compras utilizando a tarxeta propia do centro. Interpreta o intervalo obtido.
- b Se se sabe que 8 de cada 10 clientes do centro comercial utilizan para as súas compras a tarxeta propia do centro e tomamos unha mostra aleatoria de 100 clientes, ¿cal é a probabilidade de que a proporción de clientes da mostra que utilizan a tarxeta propia do centro sexa superior a 0,75?
Estimación puntual
Inferencia estatística dando só un valor.
Exemplo: Queremos coñecer cantas persoas da nosa cidade de 13 000 habitantes fuman. Para isto eliximos unha mostra de 100 persoas e obtemos que 31 delas fuman.
\[N=13000\], \[n=100\] y \[\hat{p} = 31/100 = 0.31\]
Inferimos que o número de fumadores da nosa cidade é \[N \cdot \hat{p} = 13000 \cdot 0.31 = 4030\].
Estimadores
Un parámetro mostral ou estatístico obtido co fin de estimar un parámetro poboacional.
Características desexables dos estimadores
Un estimador \[ \hat{\lambda} \] dun parámetro \[ \lambda \] agárdase que sexa
- Centrado (insesgado): \[E[\hat{\lambda}] = \lambda\]
- Eficiente: \[ VAR[\hat{\lambda}] \] é pequena.
- Consistente: mellora co aumento do tamaño da mostra.
Contraste de hipóteses
EUn fabricante garante a un laboratorio farmacéutico que as súas máquinas producen comprimidos cun diámetro medio non superior a 13 milímetros, que é o tope admitido polo laboratorio. Sábese que o diámetro dos comprimidos do fabricante segue unha distribución normal con desviación típica 0,6 milímetros. O laboratorio comproba unha mostra aleatoria de 100 comprimidos dese fabricante e obtén que o diámetro medio é 13,12 milímetros. Formula un test para contrastar que o diámetro medio dos comprimidos é o que afirma o fabricante, fronte a que é superior. A que conclusión se chega cun 5% de nivel de significación?
Hipótese nula e hipótese alternativa
- \[H_0\]: o que nos din que se cumpre.
- \[H_1\]: o contrario ao que nos din que se cumpre.
No exemplo anterior...
\[H_0: \mu \le 13 mm \\ H_1: \mu \gt 13 mm \]
Mostra e parámetro mostral
Tomamos unha mostra para contrastar \[H_0\].
No exemplo... \[n = 100\] e \[ \overline{X} = 13.12\].
Se a media desa mostra fose 20mm, credes que se verifica a hipótese nula?
Rexión de aceptación e de rechazo
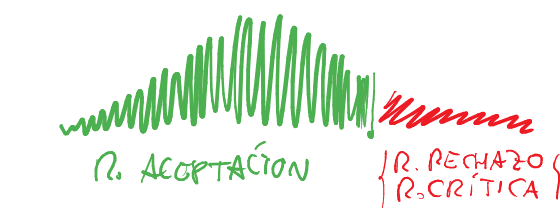
Determinamos unha rexión na que é aceptable/normal que estea a media da mostra e polo tanto unha na que non é aceptable que estea.
Nivel de significación
Denótase por \[ \alpha \] e representa a probabilidade de que sendo \[H_0\] certa, a media da mostra "caia" na rexión de rechazo.
12 Nun estudo sociolóxico afirmábase que o tempo medio que os mozos están conectados á Rede non supera as 60 horas mensuais. Deséxase contrastar se actualmente segue en vigor ese estudo e, para iso, entrevístanse 400 mozos seleccionados ao azar e obtense que o tempo medio é de 62 horas. Supoñemos que o tempo dedicado polos mozos a conectarse á Rede segue unha distribución normal, de desviación típica 15 horas mensuais.
Formula un test para contrastar a hipótese de que o tempo medio mensual dedicado actualmente polos mozos a conectarse á Rede e o que afirma o estudo, fronte á alternativa de que aumentou. ¿A que conclusión se chega cun 1% de nivel de significación?
13A información que ofrece o editor dunha escala de madurez na poboación de estudantes de ensino secundario, sinala que as puntuacións na escala seguen unha distribución normal con media 5 e desviación típica 2. A escala ten xa 10 anos, o que fai sospeitar a un educador que o promedio da escala puidera aumentar no momento actual. Para comprobalo, selecciona unha mostra aleatoria de 49 estudantes de ensino secundario e tras pasarlles a proba obtén unha media de 5,6. Supoñendo que se mantén a desviación típica, formula un test para contrastar que a puntuación media non aumentou, fronte a que si o fixo tal como sospeita o educador e explica a que conclusión se chega, cun nivel de significación do 5%
Erros
| \[H_0\] certa | \[H_0\] falsa | |
|---|---|---|
| Aceptamos \[H_0\] | BEN | Erro tipo 2 (\[ \beta \]) |
| Rechazamos \[H_0\] | Erro tipo 1 (\[\alpha\]) | BEN |
14No proceso industrial de envasado dun produto, o peso dos envases aproxímase a unha Normal de media 500 gramos e desviación típica 4 gramos. Os directivos da empresa sospeitan que a maquinaria de envasado está avariada e decidirán cambiala se o peso medio dos envases é superior a 500 gramos. Para iso, analizan contrastar unha mostra aleatoria de 30 envases e obteñen un peso medio de 501,5 gramos.
- a Formula un test para contrastar a hipótese de que non é necesario cambiar a maquinaria fronte a que si o é, tal como sospeitan os directivos, ¿a que conclusión se chega cun nivel de significación do 5%?
- b Explica o tipo de erro que cometerían se decidisen erroneamente non cambiar a maquinaria.
15Unha compañía telefónica A afirma que a proporción de fogares que contratan o seu servizo de ADSL é, polo menos, do 26%. Sen embargo, outra compañía da competencia B sostén que actualmente a proporción de usuarios da compañía A é menor do 26%. Para comprobalo fai unha enquisa a 400 clientes que teñen nos seus fogares o servizo ADSL e deles 85 manifestan que teñen contratado dito servizo á compañía A.
Formula un test para contrastar que a proporción é a que afirma a compañía A fronte á alternativa sostida pola compañía B. A que conclusión se chega cun nivel de significación do 5%?
16Nun recente estudo afírmase que hai un 5% de lesións de xeonllo entre futbolistas que xogan sobre céspede e calzan un novo modelo de botas de fútbol. De 250 futbolistas que xogan sobre céspede e que calzan botas de fútbol convencionais déronse 20 de tales lesións.
Formula un test para contrastar a hipótese de que a proporción de lesións de xeonllo xogando con botas convencionais non supera á de tales lesións xogando co novo modelo, fronte a hipótese de que si a supera.
17Unha empresa multinacional que posúe delegacións en Francia e España, realiza un estudo sobre a satisfacción dos seus empregados no traballo. Polo estudo realizado na delegación francesa, sabemos que o 45% dos empregados están satisfeitos co seu traballo. Na delegación española, dunha mostra aleatoria de 1600 empregados 672 están satisfeitos co seu traballo.
- a Formula un test para contrastar a hipótese de que a proporción de empregados satisfeitos na delegación española é polo menos a mesma que na delegación francesa fronte a que é inferior. ¿Cal sería a conclusión cun 1% de nivel de significación?
- b Explica, no contexto do problema, en que consisten os erros de tipo I e de tipo II.