Tema 2: Variables Aleatorias
Variables aleatorias
Función que asocia a cada suceso elemental, un número real.
\[ X:\Omega\to \mathbb{R} \]
Exemplo
Definimos a v.a. discreta \[X = \] "Número de caras obtidas ó lanzar 3 moedas."
- "Non sacar ninguna cara" \[\Rightarrow 0 \]
- "Sacar unha cara" \[\Rightarrow 1 \]
- "Sacar dúas caras" \[\Rightarrow 2 \]
- "Sacar tres cara" \[\Rightarrow 3 \]
Tipos
- Discretas: P. ex. "número obtido ó lanzar un dado"
- Continuas: P. ex. "altura de unha persoa elixida ó azar"
V.A. Discretas
Función de masa de probabilidade
Dada unha variable aleatoria discreta \[X\]:
\[ f(x_i) = p_i = P(X=x_i) \]
Exemplo
Definimos a v.a. discreta \[X = \] "Número de caras obtidas ó lanzar 3 moedas."
- \[ p_0 = f(0) = P(X=0) = 1/8 \]
- \[ p_1 = f(1) = P(X=1) = 3/8 \]
- \[ p_2 = f(2) = P(X=2) = 3/8 \]
- \[ p_3 = f(3) = P(X=3) = 1/8 \]
Gráfica
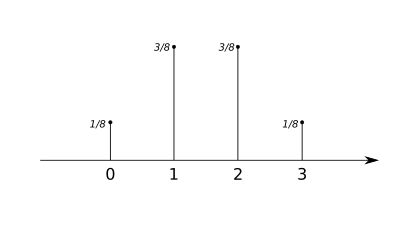
Propiedades
- \[f(x_i) \in [0, 1]\] (é unha probabilidade)
- \[ \sum_i f(x_i) = 1 \]
1Indica os valores da función de masa de probabilidade das seguintes variables aleatorias e traza a súa gráfica:
- a \[ X = \]"Número de cruces ó lanzar 2 moedas"
- b \[ Y = \]"Suma dos números obtidos ó lanzar dous dados de 4 caras"
V.A. Discretas
Función de distribución
Dada unha variable aleatoria discreta \[X\]:
\[ F(x_i) = P(X \le x_i) \]
Exemplo
Definimos a v.a. discreta \[X = \] "Número de caras obtenidas ó lanzar 3 moedas."
- \[ F(0) = P(X \le 0) = 1/8 \]
- \[ F(1) = P(X \le 1) = 4/8 \]
- \[ F(2) = P(X \le 2) = 7/8 \]
- \[ F(3) = P(X \le 3) = 8/8 = 1 \]
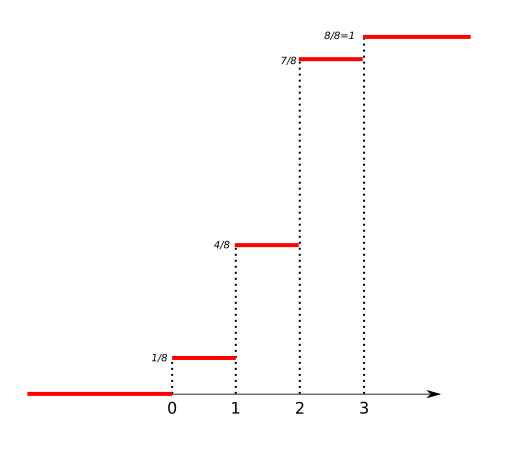
Propiedades
- \[ F(x) \in [0, 1] \]
- Función creciente
- \[ \lim_{x \to -\infty} F(x) = 0 \]
- \[ \lim_{x \to +\infty} F(x) = 1 \]
- \[ P(a \ge X \ge b) = F(b) - F(a) \]
2Indica os valores da función de distribución das seguintes variables aleatorias e traza a súa gráfica:
- a \[ X = \]"Número de cruces ó lanzar 2 moedas"
- b \[ Y = \]"Suma dos números obtidos ó lanzar dous dados de 4 caras"
Parámetros dunha v.a. discreta
Esperanza matemática ou media
Apórtanos o "valor esperado" ó realizar o experimente aleatorio.
\[ \mu_x = E[x] = \sum_i x_i \cdot f(x_i) \]
Exemplo
Definimos a v.a. discreta \[X = \] "Número de caras obtidas ó lanzar 3 moedas."
\[E[X] = \sum_i x_i \cdot f(x_i) = 0 \cdot f(0) + 1 \cdot f(1) + 2 \cdot f(2) + \]
\[+ 3 \cdot f(3) = 0 \cdot \frac{1}{8} + 1 \cdot \frac{3}{8} + 2 \cdot \frac{3}{8} + 3 \cdot \frac{1}{8} = \]
\[ = \frac{0}{8} + \frac{3}{8} + \frac{6}{8} + \frac{3}{8} = \frac{12}{8} = 1'5\]
Parámetros dunha v.a. discreta
Varianza
Apórtanos una medida de dispersión dos valores da variable con respecto á media.
\[\sigma_x^2 = VAR[X] = \sum_i (x_i - \mu)^2 \cdot f(x_i) = \]
\[= \sum_i x_i^2 \cdot f(x_i) - \mu^2 \]
\[VAR[X] = \sum_i x_i^2 \cdot f(x_i) - \mu^2 = \] \[ = 0^2 \cdot f(0) + 1^2 \cdot f(1) + 2^2 \cdot f(2) + 3^2 \cdot f(3)) - 1.5^2 =\] \[ = (0 \cdot \frac{1}{8} + 1 \cdot \frac{3}{8} + 4 \cdot \frac{3}{8} + 9 \cdot \frac{1}{8}) - 1.5^2 = \] \[ = (\frac{0}{8} + \frac{3}{8} + \frac{12}{8} + \frac{9}{8}) - 1.5^2 = \frac{24}{8} - 1.5^2 = 0.75\]
Parámetros dunha v.a. discreta
Desviación típica
Apórtanos una medida de dispersión pero nas mesmas unidades que a variable.
\[\sigma_x = \sqrt{\sigma_x^2} = \sqrt{VAR[X]}\]
\[ \sigma_x = \sqrt[\sigma_x^2] = \sqrt{0.75}= 0.86\]
3Calcula a media, varianza e desviación típica das seguintes variables aleatorias:
- a \[ X = \]"Número de cruces ó lanzar 2 moedas"
- b \[ Y = \]"Suma dos números obtidos ó lanzar dous dados de 4 caras"
4Definimos un experimento aleatorio como sigue:
Nunha bolsa temos 6 bólas: 3 bolas cun número 1 debuxado, 2 bolas cun número 2 debuxado e 1 bola cun número 3 debuxado. Sacamos dúas bolas da bolsa.
Definimos agora a variable aleatoria \[Z=\]"suma dos número de las dúas bolas".
Calcula os valores das funcións de masa de probabilidade y a de distribución, traza as súas gráficas e calcula a media, varianza e desviación tipica.
V.A. Continua
Exemplos
- \[X= \] "Lonxitude duns certos tornillos"
- \[X= \] "Tempo de vida dun certo tipo de lámpadas medido en horas"
- \[X= \] "Litros de auga consumidos por unha persona"
Función de distribución
\[ F(x) = P(X \le x) \]
Propiedades
- \[ F(x) \in [0, 1] \]
- Función creciente
- \[ \lim_{x \to -\infty} F(x) = 0 \]
- \[ \lim_{x \to +\infty} F(x) = 1 \]
- \[ P(a \ge X \ge b) = F(b) - F(a) \]
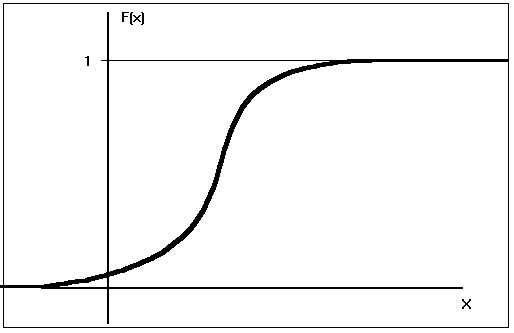
Cal é a probabilidade de que unha persoa mida exactamente 1,72m?
Función de densidade
\[f(x)\]
Versión suavizada del histograma



Propiedades
- \[f(x) \in [0, 1]\] (es una probabilidade)
- \[ \int_{-\infty}^{\infty} f(x) = 1 \]
Media ou esperanza matemática
| V.A. Discreta | V.A. Continua |
|---|---|
| \[\sum_i x_i \cdot f(x_i)\] | \[\int_{-\infty}^{\infty} x \cdot f(x) dx\] |
Varianza
| V.A. Discreta | V.A. Continua |
|---|---|
| \[\sum_i (x_i - \mu)^2 \cdot f(x_i)\] \[\sum_i x_i^2 \cdot f(x_i) - \mu^2 \] |
\[\int_{-\infty}^{\infty} (x - \mu)^2 \cdot f(x) dx\] \[\int_{-\infty}^{\infty} x^2 \cdot f(x) dx - \mu^2 \] |
Desviación típica
\[\sigma_x = \sqrt{\sigma_x^2} = \sqrt{VAR[X]}\]
Distribuciones notables
Distribuciones notables: variables discretas
Chamamos proceso de Bernuilli a un experimento no que:
- Cada observación é independiente.
- Cada observación pódese clasificar en só dúas categorías: éxito ou fracaso.
- As probabilidades de éxito e fracaso son consantes e denótanse por \[p\] e \[q\].
Exemplos de procesos de Bernuilli
- Un exame tipo test consta de 10 preguntas, cada unha con 4 respostas das cales só unha é correcta.[...] (Mat. 2018)
- Nun bombo temos 10 bolas idénticas numeradas do 0 ao 9 e cada vez que facemos una extracción devolvemos a bola ao bombo [...] (Mat. 2018)
Distribución Binomial
Dicimos que unha variable aleatoria discreta segue unha distribución Binomial cando, traballando cun proceso de Bernuilli, é da forma:
\[X\]="Número de éxitos en \[n\] intentos"
Denotándoo por \[X \sim B(n,p)\]
Exemplos
Un exame tipo test consta de 10 preguntas, cada unha con 4 respostas das cales só unha é correcta. Cal é a probabilidade de contestar ben polo menos dúas preguntas? (Mat. 2018)
\[X=\] "Número de preguntas ben contestadas." \[X \sim B(10, 0.25)\]
Exemplos
Nun bombo temos 10 bolas idénticas numeradas do 0 ao 9 e cada vez que facemos una extracción devolvemos a bola ao bombo. Se facemos 5 extraccións, calcula a probabilidade de que o 7 saia menos de dúas veces.(Mat. 2018)
\[X=\] "Número de 7 sacados" \[X \sim B(5, 0.1)\]
5 Dado experimento aleatorio "lanzar 3 dados de 5 caras", pregúntannos pola probabilidade de obter dúas veces un 3. Defíne a variable aleatoria coa que imos a traballar. Indica que probabilidade nos preguntan e calcúlaa co que sabes do tema anterior.
Función de masa de probabilidad
Dada unha variable aleatoria \[X \sim B(n,p)\]
\[f(k) = P(X = k) = \binom{n}{k} \cdot p^k \cdot q^{n-k}\]
Coeficiente binomial
\[\binom{n}{k} = \frac{n!}{k! (n-k)!}\]

Función de distribución
Dada unha variable aleatoria \[X \sim B(n,p)\]
\[F(k) = P(X \le k) = \sum_{i \le k} f(i) \]
\[F(2) = f(0) + f(1) + f(2)\]
Dada una variable aleaatoria \[X \sim B(n,p)\]
Esperanza matemática o media: \[E[X] = np \]
Varianza: \[VAR[X] = npq \]
6A probabilidade de que un home acerte no branco é 0'25. Se dispara 10 veces, cal é a probabilidade de que acerte exactamente en tres ocasións? Cal é a probabilidade de que acerte polo menos nunha ocasión?
7Nunha asociación xuvenil o 60% dos socios xogan ao balonmán. Nun momento dado trátase de reunir xente para formar un equipo, polo que se pregunta a un grupo de 20 socios se practican o dito deporte. Cal é a probabilidade de que no grupo haxa tres o máis persoas que xoguen ao balonmán?
8O 85% da población considera que os tratamentos de psicoterapia son caros. Elixida unha mostra ao azar formada por sete individuos. ¿cuál é a probabilidade de que todos os consideren caros? e de que ningún os considere caros? e de que polo menos tres os consideren caros?
9Un examen tipo test consta de 10 preguntas, cada unha con 4 respostas das cales só unha é correcta. Se se contesta ao chou, cal é a probabilidade de contestar ben polo menos dúas preguntas? (MAT - Xuño 2018)
10En Sargadelos prodúcense un 10% de pezas con algún defecto. Se a fábrica produce ao día 50 pezas, cal é a probabilidade de que haxa menos de 5 pezas defectuosas? Calcula a media e a varianza da distribución.
Distribución Normal
- Distribución continua
- Ten por parámetros a media \[\mu\] e a desviación típica \[ \sigma \] da distribución.
- Lo denotamos por \[ X \sim N(\mu, \sigma) \]
Función de densidade
\[f(x) = {1 \over \sigma\sqrt{2\pi}} e^{-(x-\mu)^2 / 2\sigma^2}\]

Características
- Área baixo a curva é 1 (é unha función de densidade).
- Máximo en \[x = \mu\]
- Simétrica (par) con respecto a recta \[x = \mu\]
Función de distribución
\[F(x) = \int_{-\infty}^x f(x) dx\]

Distribución normal tipificada
- \[Z \sim N(0,1)\]
- Su función de distribución está tabulada \[\Phi(z)\]
ECalcula as seguintes probabilidades para \[Z \sim N(0,1)\]:
- a \[P(Z \lt 0'63)\]
- b \[P(Z \gt 0'63)\]
- c \[P(Z \lt -0'63)\]
- d \[P(Z \gt -0'63)\]
- e \[P(0'34 \gt Z \gt 0'76)\]
11Calcula as seguintes probabilidades para \[Z \sim N(0,1)\]:
- a \[P(Z \lt 0'88)\]
- b \[P(Z \lt 0'74)\]
- c \[P(Z \gt 0'23)\]
- d \[P(Z \lt -0'57)\]
- e \[P(Z \gt -0'8)\]
- f \[P(Z \lt 2'34)\]
- g \[P(Z \gt 2'4)\]
- h \[P(Z \lt -1'23)\]
- i \[P(0'23 \lt Z \lt 0'63)\]
- j \[P(-0'45 \lt Z \lt 0'38)\]
- k \[P(-0'43 \lt Z \lt -0'13)\]
- l \[P(0'83 \lt Z \lt 1'22)\]
Tipificación de variable aleatoria
Sexa \[X \sim N(\mu, \sigma)\] podemos facer o cambio de variable \[Z = \frac{X - \mu}{\sigma}\]
P. ex: Dada \[X \sim N(13, 3'4)\]
\[P(X \lt 24) = P(Z \lt \frac{24 - 13}{3'4}) = \\ = P(Z \lt 2'23) = \Phi(2'23)\]
12Calcula as seguintes probabilidades:
- a \[P(X \lt 38'23)\] con \[X \sim N(20, 12'3)\]
- b \[P(X \lt 6'42)\] con \[X \sim N(2, 5'6)\]
- c \[P(X \lt -20)\] con \[X \sim N(-12, 3'4)\]
- d \[P(X \lt -4)\] con \[X \sim N(0, 8)\]
- e \[P(X \lt 130'5)\] con \[X \sim N(120, 30)\]
- f \[P(X \lt 14'8)\] con \[X \sim N(13, 0'7)\]
13Nun determinado lugar, a temperatura máxima durante o mes de xullo segue unha distribución normal de media 25°C e desviación típica 4°C. Calcula a probabilidade de que a temperatura máxima dun certo día estea comprendida entre 21°C e 27.2°C.
14Un saltador de lonxitude salta unha media de 8 metros con desviación típica de 20 cm. Para poder ir á próxima olimpíada é necesario ter unha marca de 8’30 metros, ¿Que probabilidade ten de conseguir esta marca nun salto? E, ¿cal é esta probabilidade se realiza dez saltos?
15 Unha fábrica produce pezas cuxo grosor segue unha distribución normal de media 8 cm e desviación típica 0.01 cm. Calcula a probabilidade de que unha peza teña un grosor comprendido entre 7.98 e 8.02 cm.
16 O total de vendas diarias nun pequeno restaurante é unha variable que segue unha distribución normal de media 1220€ ao día e desviación típica 120€ ao día. Calcula a probabilidade de que nun día elixido ao azar as vendas excedan de 1400€.
17 A vida útil dunha marca de lámpadas segue unha distribución normal de media 1.200 horas de desviación típica 250 horas. Que proporción de lámpadas ten un tempo de vida inferior a 1.050 horas?, que proporción de lámpadas ten un tempo de vida superior a 1.350 horas? Explique brevemente o porqué da relación entre os resultados. Que proporción de lámpadas ten un tempo de vida entre 1.050 e 1.350 horas?
Aproximación da distribución Binomial coa distribución Normal
Se vemos o histograma da normal...
Geogebra...Cando \[n\] é moi grande podemos aproximar unha distribución binomial con parámetros \[n\] e \[p\] por unha Distribución Normal de media \[\mu = n \cdot p\] e desviación tipica \[\sigma = \sqrt{n \cdot p \cdot q}\]
18Cal é a distribución binomial que empregamos no seguinte problema e como a podemos aproximar pola Normal:
Nun bombo temos 10 bolas idénticas numeradas do 0 ao 9 e cada vez que facemos una extracción devolvemos a bola ao bombo. Se facemos 100 extraccións, calcula a probabilidade de que o 7 saia menos de 12 veces.
Corrección de Yates / De continuidad
Ao aproximar unha variable discreta (Binomial) por unha continua (Normal) debemos facer una corrección de medio punto sobre os valores a calcular. É dicir, debemos sumar o restar 0'5 ós valores nos que estamos calculando a probabilidade.
EJEMPLO: Dada la variable \[X \sim B(100, 0'3)\] nos piden calcular la probabilidad \[P(X \ge 9)\] aproximandola por la distribución Normal.
- Aproximaríamos la distribución: \[B(100,0'3)\] por \[N(30, 7)\].
- Aplicaríamos la corrección de Yates: \[P(X \ge 9) \approx P (X \ge 8'5)\]
- Tipificaríamos la variable \[X\] y calcularíamos la probabilidad usando las tablas de la distribución normal tipificada
19Nun bombo temos 10 bolas idénticas numeradas do 0 ao 9 e cada vez que facemos una extracción devolvemos a bola ao bombo
- a Se facemos 5 extraccións, calcula a probabilidade de que o 7 saia menos de dúas veces.
- b Se facemos 100 extraccións, calcula a probabilidade de que o 7 saia menos de nove veces.
20 A probabilidade de que un determinado xogador de fútbol marque gol desde o punto de penalti é . Se lanza 5 penaltis, calcula as seguintes tres probabilidades: de que non marque ningún gol; de que marque polo menos 2 goles; e de que marque 5 goles. Se lanza 2100 penaltis, calcula a probabilidade de que marque polo menos 1450 goles. Estase a asumir que os lanzamentos son sucesos independentes.
21Sábese que o 10% dos alumnos de Bacharelato son fumadores. En base a isto, calcule a probabilidade aproximada de que, polo menos, haxa 310 alumnos fumadores dos 3.000 que se presentan ó exame de selectividade.
Busca inversa distribución Normal
22Calcula \[a\] nos seguintes casos se \[Z \sim N(0,1)\]:
- a \[P(Z\lt a) = 0.9345\]
- b \[P(Z \lt a) = 0.9828\]
- c \[P(Z \gt a) = 0.3427\]
- d \[P(Z \lt a) = 0.2745\]
- e \[P(-a \lt Z \lt a) = 0.95\]
- f \[P(-a \lt Z \lt a) = 0.98\]
23Calcula \[a\] nos seguintes casos:
- a \[P(X \lt a) = 0.8345\] con \[X \sim N(22, 3) \]
- b \[P(X \lt a) = 0.8945\] con \[X \sim N(100, 12) \]
- c \[P(X \gt a) = 0.2345\] con \[X \sim N(10, 2,5) \]
- d \[P(Z \lt a) = 0.4356\] con \[X \sim N(0, 3) \]