Tema 1
Números reales
Conjuntos numéricos
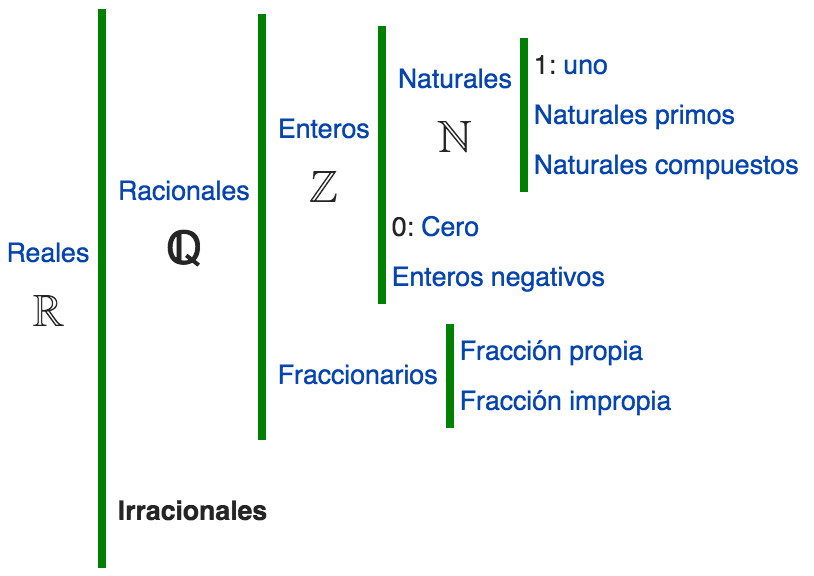
1Clasifica los siguientes números en naturales, enteros, racionales o irracionales:
- 25,37 \[ \in \mathbb{Q} \]
- -6/17 \[ \in\mathbb{Q} \]
- 2/5 \[ \in \mathbb{Q} \]
- \[-\sqrt{12}\] \[ \in \mathbb{I} \]
- \[ \pi \] \[ \in \mathbb{I} \]
- -5 \[ \in \mathbb{Z} \]
Valor absoluto
Si \[x \in \mathbb{R}\], \[|x|\] es distancia en la recta real de x al 0.
Valor absoluto: propiedades
- \[|a| \ge 0 \]
- \[|a \cdot b| = |a| \cdot |b| \]
- \[d(a,b) = |a - b|\] (nos permite calcula la distancia entre dos puntos en al recta real)
2Indica el valor absoluto de los siguientes números:
- \[|-3|
- \[|2|\]
- \[|5|\]
- \[|-1|\]
Intervalos, semirectas y entornos
Son subconjuntos continuos de la recta real.- Intervalos: indicamos principio y fin
- Semirectas: indicamos principio o fin. El otro extremo es \[\pm \infty\].
- Entornos: indicamos centro y radio
Intervalos y semirectas
- Abierto: no incluímos el extremo. Se indica con paréntesis (2,5)
- Cerrado: incluímos el extremo. Se indica con corchetes [-6,10]
3Representa como intervalos los siguientes conjuntos de números:
- \[\{x \in \mathbb{R} / -1 \le x \lt 5 \} \] = [-1, 5)
- \[\{x \in \mathbb{R} / -1 \ge x \gt -5 \} \] = (-5,-1]
- \[\{x \in \mathbb{R} / -3 \lt x \} \] \[= (-3, \infty) \]
- \[\{x \in \mathbb{R} / 3 \gt x \} \] \[= (-\infty, 3) \]
- \[\{x \in \mathbb{R} / -1 \le x \le 0 \} \] \[= [-1,0] \]
Operaciones con conjuntos: unión e intersección
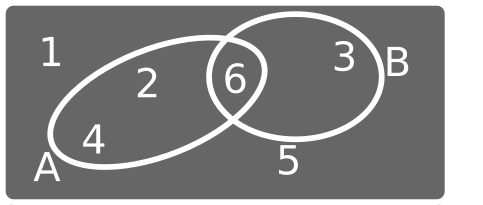
Unión
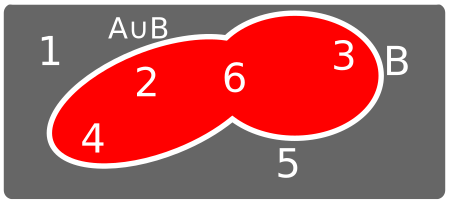
Intersección

Unión e intersección de intervalos
4Dados \[A=(2,4)\], \[B=(-2,4)\] y \[C=(-3, \infty)\], calcula:
- \[A \cup B \cup C\]
- \[A \cap B \cap C\]
- \[(A \cap B) \cup C\]
- \[(A \cup B) \cap C\]
Entornos
Indicamos el centro y el radio
\[E(3,4) =\{x \in \mathbb{R} / |x-3| \lt 4 \} = (-1, 7)\]

Entornos
- Entornos abiertos: se incluyen los extremos. \[E(3, 10)\]
- Entornos cerrados: no se incluyen los extremos. \[E[-2, 5]\]
5Expresa como entornos los intervalos \[(-5, 2)\] y \[[-10, 10]\]
6Expresa como intervalos los siguientes entornos:
- \[E(5,2)\]
- \[E(10,13)\]
- \[E[0,4.5]\]
Aproximación de números reales
- Redondeo
- Truncamiento
7Aproxima los siguientes números como se indica:
- Redondea a las centésimas el número 12,23563
- Trunca a las décimas el número 9,2934
Cálculo de errores
- Error absoluto: \[ E_a = |V_{\text{real}} - V_{\text{aproximado}} | \]
- Error relativo: \[ E_r = \frac{E_a}{V_{\text{real}}}\]
8Calcula el error absoluto y el error relativo cometido al aproximar el número \[\sqrt{2}\] por \[1,4\].
Notación científica

9Escribe, utilizando notación científica, estos números:
- a Distancia Tierra-Luna: 384000Km \[ = 3,84 \cdot 10^5 \]
- b Superficie de la tierra: 150000000 km² \[ = 1,5 \cdot 10^8 \]
- c Longitud de un virus (gripe): 0,0000000022 m \[ = 2,2 \cdot 10^{-9} m \]
- d Peso de un estafilococo: 0,0000001g \[ = 1 \cdot 10^{-7} g \]
Operaciones con Not. Científica
- Multiplicación / División
- Suma / Resta
10 Realiza las siguientes operaciones con números en notación científica:
- a \[ 6,342 \cdot 10^4 + 5,34 \cdot 10^{-1} \] \[= 6,3420534 \cdot 10^4\]
- b \[ 8,452 \cdot 10^{-6} - 7,24 \cdot 10^{-8} \] \[= 8,3796 \cdot 10^{-6}\]
- \[ 8,452 \cdot 10^{-6} \cdot 7,24 \cdot 10^{-8} \] \[= 6,119248 \cdot 10^{-13}\]
- \[ 3,43 \cdot 10^3 : 2,45 \cdot 10^{-2} \] \[= 1,4 \cdot 10^5\]
Radical
\[ \sqrt[n]{a} = b \iff b^n = a \]Por exemplo \[\sqrt[3]{8} = 2\] porque \[2^3\]
Propiedades
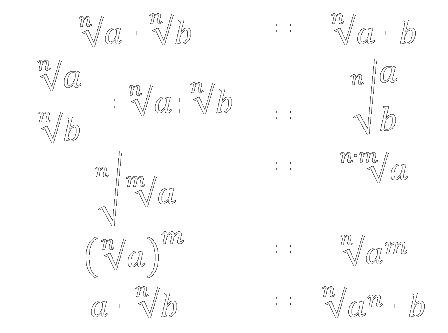
11Extrae factores de los siguientes denominadores:
- \[ \sqrt{3^{10} \cdot 5^7 \cdot 7 \cdot 13^2}\]
- \[ \sqrt[3]{3^{10} \cdot 5^6 \cdot 7^2 \cdot 13^3} \]
12Introduce los siguientes factores en el radical:
- \[ 2 \cdot 3^2 \sqrt{5}\]
- \[ 2 \cdot 3^2 \sqrt[5]{5^3}\]
13Simplifica las siguientes expresiones
- \[ \sqrt{2} + \frac{3}{2} \sqrt{8} - \frac{1}{4}\sqrt{18} \]
- \[ \sqrt[4]{144 a^2} - 2 \sqrt{\frac{27}{16} a} + \sqrt{3a} \]
- \[ \frac{a^4 \sqrt[3]{a^2}(\sqrt{a})^3}{\sqrt{\sqrt[3]{a^5}}} \]
Racionalizar
Eliminar las raíces del denominador
14Racionaliza los siguientes denominadores:
- \[ \frac{5}{2\sqrt{5}} \]
- \[ \frac{5}{2\sqrt[4]{5}} \]
- \[ \frac{5}{2\sqrt{5} + 1} \]
- \[ \frac{\sqrt{6}}{2\sqrt{3} - 3\sqrt{2}} \]
Logaritmos
\[ log_a (b) = c \iff a^c = b \]
15Aplicando la definición, halla el valor de los logaritmos:
- \[log_3 27 \]
- \[log_3 \sqrt{27} \]
- \[log_5 \sqrt[3]{25} \]
- \[log_7 \frac{1}{49} \]
- \[log_9 \sqrt[3]{3} \]
- \[log_3 0,\widehat{3} \]
Propiedades de los logaritmos
\[log_a (b \cdot c) = log_a (b) + log_a (c)\]
\[log_a (b^n) = n \cdot log_a (b)\]
\[log_a (\frac{b}{c}) = log_a (b) - log_a (c)\]
\[log_a b = \frac{log_x b}{log_x a}\]
16Factoriza y aplica las propiedades de los logaritmos para expresar en función de suma ou resta de logaritmos de números primos:
- \[ log~2^4 \cdot 3 - log 2^3 \cdot 3^4 \]
- \[ log 24 + log \frac{16}{9} - log 144 \]
- \[ log~686 + log~56 - log~\frac{16}{49} \]
- \[ log~100 - log \frac{8}{25} + log~250 \]
17Expresa el valor de E en cada caso sin que aparezcan logaritmos:
- \[log E = log~x + 2 log~y - log~z\]
- \[log E = 3(log x -1) - 2(1-log y)\]
- \[log E = 2 log\sqrt{x} - log x - log y + 3 log \sqrt[3]{y}\]
- \[log E = log x^3 + 3 log y - log x^4\]
Ampliación: Tipos de números decimales
Existen decimales exactos (como \( 0.75 \)), periódicos puros (como \( 0.\overline{3} \)) y periódicos mixtos (como \( 0.1\overline{6} \)).
* Indica de qué tipo son los siguientes decimales:
- \( 0.5 \)
- \( 0.\overline{7} \)
- \( 0.12\overline{3} \)
- \( \pi = 3.14159265359 \dots \)
Ampliación: Conversión a números decimales
De fracción a decimal
Para convertir una fracción a decimal, divide el numerador entre el denominador.
De decimal a fracción (decimales exactos)
Para convertir un decimal exacto a fracción, escribe el número como un cociente y simplifica.
De decimal a fracción (decimales periódicos)
Para convertir un decimal periódico a fracción, usa el método algebraico para despejar.
* Transforma los siguientes decimales periódicos a fracción:
- \( 3.\overline{5} \)
- \( 0.\overline{23} \)
- \( 41.\overline{041} \)
- \( 6.2\overline{5} \)
- \( 0.00\overline{1} \)
- \( 5.0\overline{18} \)
- \( 5.\overline{03} \)
Ampliación: Pasar de conjuntos a intervalos y entornos:
*Transforma en un intervalo, unión de intervalos o un entorno:
- $\{x \in \mathbb{R} \;|\; |x - 4| < 6\}$
- $\{x \in \mathbb{R} \;|\; |x + 2| \leq 5\}$
- $\{x \in \mathbb{R} \;|\; |x - 7| > 3\}$
- $\{x \in \mathbb{R} \;|\; |x + 1| \geq 8\}$
- $\{x \in \mathbb{R} \;|\; |x - 10| < 4\}$
- $\{x \in \mathbb{R} \;|\; |x + 6| \leq 2\}$
Ampliación: Cotas de error absoluto y relativo al aproximar
El error absoluto \[E_a\] y relativo \[E_r\] cometidos al aproximar por redondeo serán los siguientes:
\[E_a \lt \epsilon = \frac{1}{2 \cdot 10^n} \]
\[E_r < \frac{\epsilon}{V_{aproximado} - \epsilon}\]
*Indica una cota del error absoluto y relativo de los siguientes redondeos:
- El número \[\pi\] a las décimas.
- El número \[1234,254\] a las centenas.
- El número \[\sqrt{2}\] a las milésimas.