Tema 8
Números Complejos
Concepto de números complejos
\[x^2 + 1 = 0\]
El conjunto de los números complejos
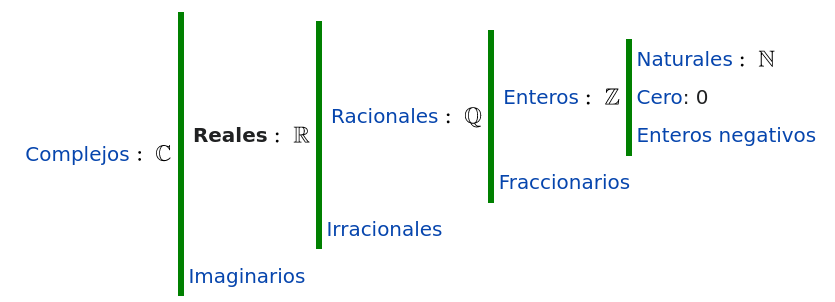
\[ \mathbb{C} \subset \mathbb{R} \]Clasificación números
La constante \[i\]
\[i = \sqrt{-1}\]
\[x^2 +1 = 0\]
\[x = \pm~i \]
Forma Binómica
\[z = a + b \cdot i\]
1Resuelve las siguientes ecuaciones usando números complejos en forma binómica:
- \[x^2+4 = 0 \]
- \[x^2 + 10x +26 = 0 \]
- \[x^2 -4x +13 = 0\]
Forma Binómica: Parte Real/Imaginaria
\[z = a + b \cdot i\]
\[Re(z) = a\]
\[Im(z) = b\]
2Identifica la parte real e imaginaria de los complejos del ejercicio anterior.
Representación de los números complejos
Plano complejo
3Representa en el plano complejo los números complejos del apartado anterior
Forma polar
Módulo y argumento
- \[ |z| = \] \[\sqrt{a^2 + b^2}\]
- \[ arg(z) = \] \[arctan(\frac{b}{a})\]
4Pasa los siguientes números complejos a forma polar:
Paso de Polar a Binómica
- \[ a = Re(z) = \]
- \[ b = Im(z) = \]
Forma trigonométrica
\[ z = |z| \cdot (cos(\alpha) + i \cdot sen(\alpha)) \]5Pasa los siguientes números complejos en forma Polar a forma trigonométrica y despues a forma binom