Tema 7
Semejanza y trigonometría
Ángulo
Grados sexagesimales
Un ángulo completo de una circunferencia mide 360º
Radián
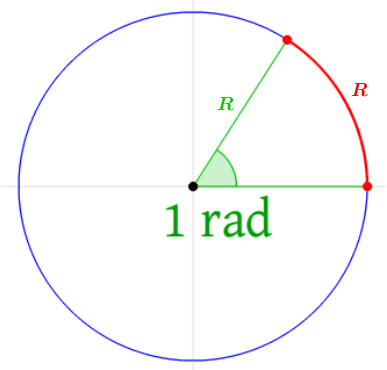
Radián
Un radián es el ángulo central de una circunferencia que abarca un arco de igual longitud que el radio de la misma.
Un angulo completo de una circunferencia mide \[2 \pi~rad\].
1Pasa de radianes a grados sexagesimales y viceversa:
- a 30º
- b 90º
- c \[\frac{2\pi}{3}~rad\]
Clasificación ángulos
- Ángulo nulo (0º)
- Ángulo agudo (\[\lt 90º\])
- Ángulo recto (90º)
- Ángulo obtuso (\[\gt 90º\])
- Ángulo llano (180º)
- Ángulo completo (360º)
Ángulos: definiciones
- Ángulos consecutivos: comparten un vértice y un lado.
- Ángulos complementarios: suman 90º
- Ángulos suplementarios: suman 180º
- Ángulos opuestos por el vértice: los lados de uno son semirectas opuestas del otro.
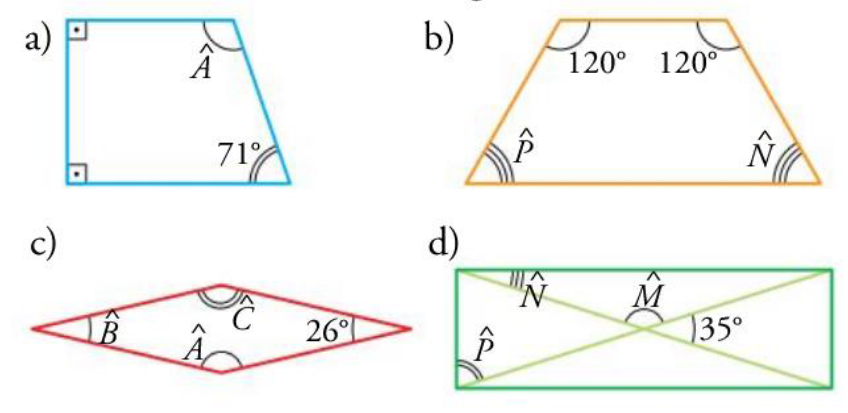
Ángulos y polígonos
Los ángulos de un polígono de \[n\] lados suman \[180º\cdot (n-2)\].
Los de un triángulo por lo tanto 180º y los de un cuadrilátero 360º.
2Calcula el valor de los ángulos que faltan:
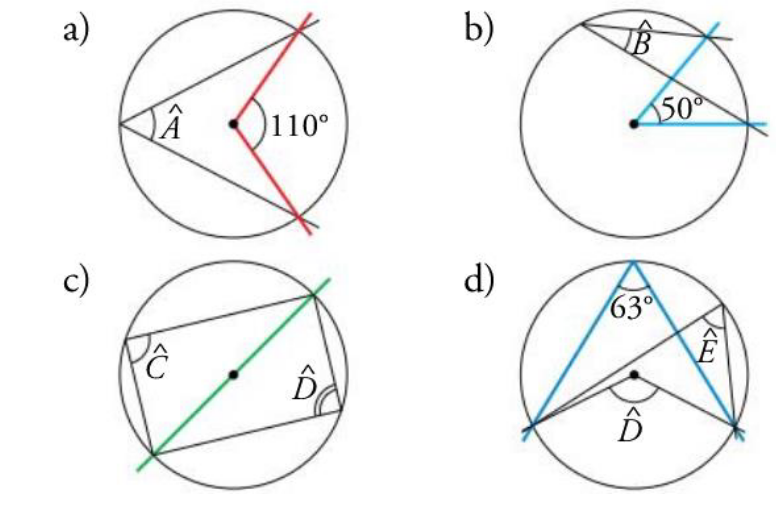
Ángulos y circunferencia
- Ángulo central: tiene por vértice el centro de la circunferencia.
- Ángulo inscrito: tiene su centro en la circunferencia.
La medida del ángulo inscrito es la mitad del ángulo central que abarca.
3Calcula el valor de los ángulso que faltan:
Proporcionalidad directa y razón de proporcionalidad
Dos magnitudes son directamente proporcionales si el cociente entre ellas es constante. Dicha constante se denomina razón de proporcionalidad.
4Dadas dos magnitudes X e Y directamente proporcionales y conocida \[k = \frac{X}{Y}=3 \] su razón de proporcionalidad, completa la siguiente tabla:
| X | 18 | |
|---|---|---|
| Y | 10 |
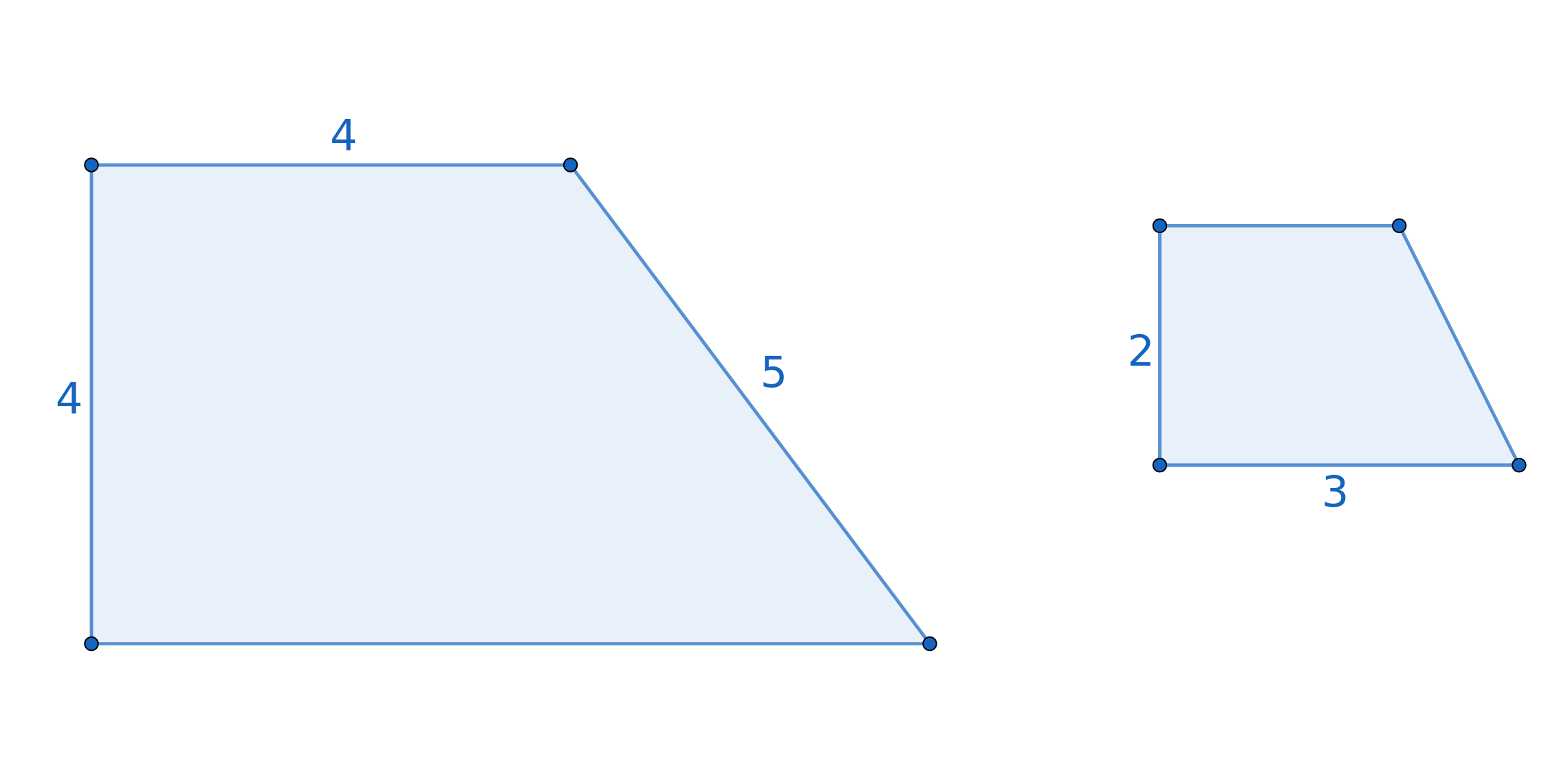
Semejanza
Dos polígonos son semejantes si sus ángulos son iguales y sus lados proporcionales. La razón de proporcionalidad se llama en este caso razón de semejanza.
5Calcula las medidas de los lados que faltan sabiendo que son figuras semejantes:
Semejanza: área y volumen
Si \[k\] es la razón de semejanza de dos figuras geométricas, su area tiene razón de semejanza \[k^2\] y su volumen tiene razón de semejanza \[k^3\].
6Calcula el volumen y la superficie lateral de las figuras semejantes a las dadas con razón de proporcionalidad 2.
Un uso de la semajanza: escalas
Una escala se indica con una razón de la forma 1:20 donde se indica que cada unidad del plano o de la maqueta se corresponde con 20 unidades de la realidad que pretenden representar.
6En un mapa cuya escala es 1:1 500 000, calcula:
- La distancia real entre dos ciudades que en el plano las separan 2,5cm.
- La distancia en el plano de dos ciudades cuya distancia real es de 360Km.
- La superficie real de una cuadrícula del plano que mide 3x3cm.
7Indica, en cada caso la escala del plano:
- 1 mm del plano representa 10m reales
- 50Km reales se representan por 1dm del plano.
Triángulos semejantes: Teorema de Tales
Dos triángulos en posición de tales son semejantes y por tanto sus lados son proporcionales.
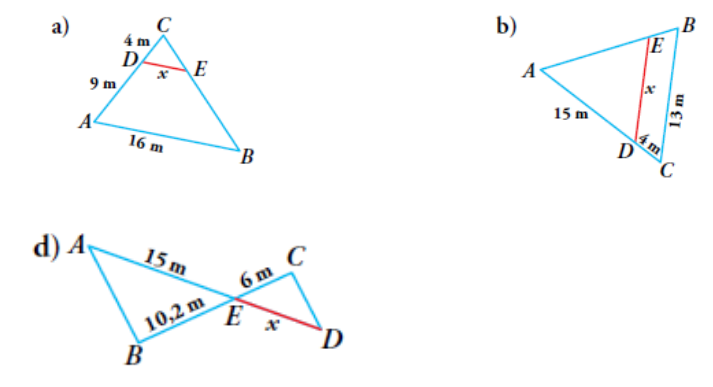
8Calcula en cada caso la longitud del segmento DE:
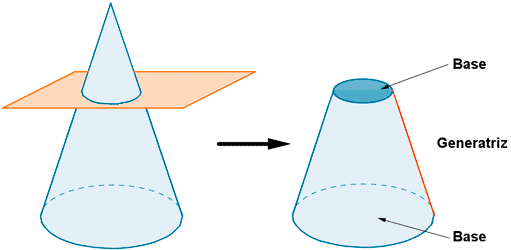
Aplicación de Tales: cálculo del volumen de un tronco de cono/pirámide
Aplicación de Tales: cálculo del volumen de un tronco de cono/pirámide
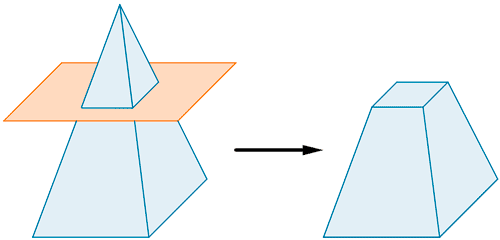
9Usando el teorema de Tales, calcula el volumen de los siguientes troncos de conos/pirámide:
- Tronco de pirámide base cuadrangular. El lado de las bases son 8cm y 6cm y la altura del tronco de pirámide es 3.
- Tronco de pirámide de base hexagonal donde la altura es 10cm y las bases tiene de lado 20cm y 14cm respectivamente. (el lado y el radio de un hexágono es el mismo)
- Tronco de cono con bases de radios 10cm y 8cm y altura del tronco 5cm.
Aplicación del Teorema de Tales: calculo de altura por sombra
10Se desea calcular la altura de un arbol para lo cual a una determinada hora del día se mide la sombra que proyecta dando como resultado 2,37m. A la misma hora se mide la sombra que proyecta una estaca de 163cm dando por resultado 76cm
Triángulos semejantes: Teorema de Tales
Dos triángulos en posición de tales son semejantes y por tanto sus lados son proporcionales.
Calcula en cada caso la longitud del segmento DE:

Razones trigonométricas
Ver en GeogebraRazones trigonométricas de un ángulo agudo
- \[ sen(\alpha) = \frac{\text{cateto opuesto}}{\text{hipotenusa}}\]
- \[ cos(\alpha) = \frac{\text{cateto contiguo}}{\text{hipotenusa}}\]
- \[ tan(\alpha) = \frac{\text{cateto opuesto}}{\text{cateto contiguo}}\]
11Dado los triángulos rectángulos siguientes, calcula la razones trigonométricas (seno, coseno y tangente) de sus ángulos agudos:
- a Catetos de 3 cm y 8 cm.
- b Un cateto de 5 cm y una hipotenusa de 10 cm.
12Calcula el seno, el coseno y la tangente de los ángulos 30º, 60º e 45º (ou \[\frac{\pi}{6}\], \[\frac{\pi}{4}\] e \[\frac{\pi}{3}\] rad) partiendo de un triángulo rectángulo isósceles y de un triángulo equilátero partido por la mitad. A los lados de estos triángulos puedes darles un valor o hacerlo con el valor genérico \[l\].
Resolución de triángulos
Resolver un triángulo consiste en conocer el valor de sus lados y de sus ángulos.
Resolución de triángulos rectángulos
Teorema e Pitágoras
Inversas de las funciones trigonométricas
Inversas de las funciones trigonométricas
13Resuelve los siguientes triángulos:
- a \[\widehat{A} = \pi/2~rad; b = 7~cm; c = 4~cm \]
- b \[\widehat{A} = \pi/2~rad; b = 5~cm; c = 9~cm \]
- c \[\widehat{A} = \pi/2~rad; a = 8~cm; b = 3~cm \]
- d \[\widehat{A} = \pi/2~rad; a = 11~cm; b = 6~cm \]
14Resuelve los siguientes triángulos:
- e \[\widehat{A} = 90º; \widehat{C} = 60º; c = 7~cm \]
- f \[\widehat{A} = 90º; \widehat{C} = 30; c = 2~cm \]
- g \[\widehat{A} = 90º; \widehat{B} = 45º; c = 7~cm \]
- h \[\widehat{A} = 90º; \widehat{C} = 60º; c = 9~cm \]
Relación entre razones trigonométricas
\[sen^2 (\alpha) + cos^2 (\alpha) = 1 \]
\[tan(\alpha) = \frac{sen(\alpha)}{cos(\alpha)} \]
\[ 1 + tan^2(\alpha) = \frac{1}{cos^2 (\alpha)}\]
15Calcula todas las razones trigonométricas (seno, coseno, tangente) a partir de la dada. Considera que todas son positivas:
- a \[ sen(\alpha) = 0,45 \]
- b \[ cos(\beta) = 0,56 \]
- c \[ tan(\gamma) = 1,2 \]
Circunferencia goniométrica
Razones trigonométricas de un ángulo cualquiera
16Indica en que cuadrante está cada uno de los siguientes ángulos y el signo de sus razones trigonométricas (seno, coseno y tangente):
- a \[ 100º \]
- b \[ 5\pi/8 rad \]
- c \[ 300º \]
Relación entre razones trignométricas de ángulos
- Ángulos suplementarios: suman 180º (\[ \pi rad \])
- Ángulos complementarios: suman 90º (\[ \frac{\pi}{2} rad \])
- Ángulos opuestos: suman 360º (\[2 \pi rad \])
17Deduce la relación entre dos ángulos que se diferencian en 90º y 180º empleando el razonamiento seguido en la explicación anterior.
Razones trigonométricas de ángulos mayores de 360º (\[2 \pi rad \])
18Calcula las siguientes razones expresándolas en función del valor de ángulos del primer cuadrante
- a \[ sen(1200º) \]
- b \[ cos(870º) \]
- c \[ tan(930º) \]
- d \[ tan(1770º) \]
- e \[ sen(960º) \]
- f \[ cos(600º) \]
- g \[ tan(2145º) \]
- h \[ tan(1120º) \]
Razones trigonométricas de ángulos comunes
| 0º | 30º | 45º | 60º | 90º |
180º | 270º | 360º | |
|---|---|---|---|---|---|---|---|---|
| sen |
||||||||
| cos |
||||||||
| tan |