Tema 5
Sistemas de ecuaciones e inecuaciones
Ecuación de dos incógnitas: solución
1Indica para cuales de las siguientes ecuaciones es solución el par \[x=2\] e \[y=3\]
- a \[ 2x - 3y = -5 \]
- b \[ x - 3y = 8 \]
- c \[ 4x - y = 5 \]
Sistema de ecuaciones
Un conjunto de varias ecuaciones.
Solución de un sistema de ecuaciones
Conjunto de números que son solución de todas las ecuaciones del sistema.
2Comprueba si \[ x = 2 \] y \[ y = 3 \] son soluciones de los siguientes sistemas:
- a \[ \begin{cases} x+5y = -1 \\ 3x-2y = 14 \end{cases} \]
- b \[ \begin{cases} 2x+3y = 21 \\ -x + y = 1 \end{cases} \]
- c \[ \begin{cases} 5x-3y = 1 \\ 4x + y = 11 \end{cases} \]
Sistemas de ecuaciones lineales
Tipos de S.E.L. según nº de soluciones
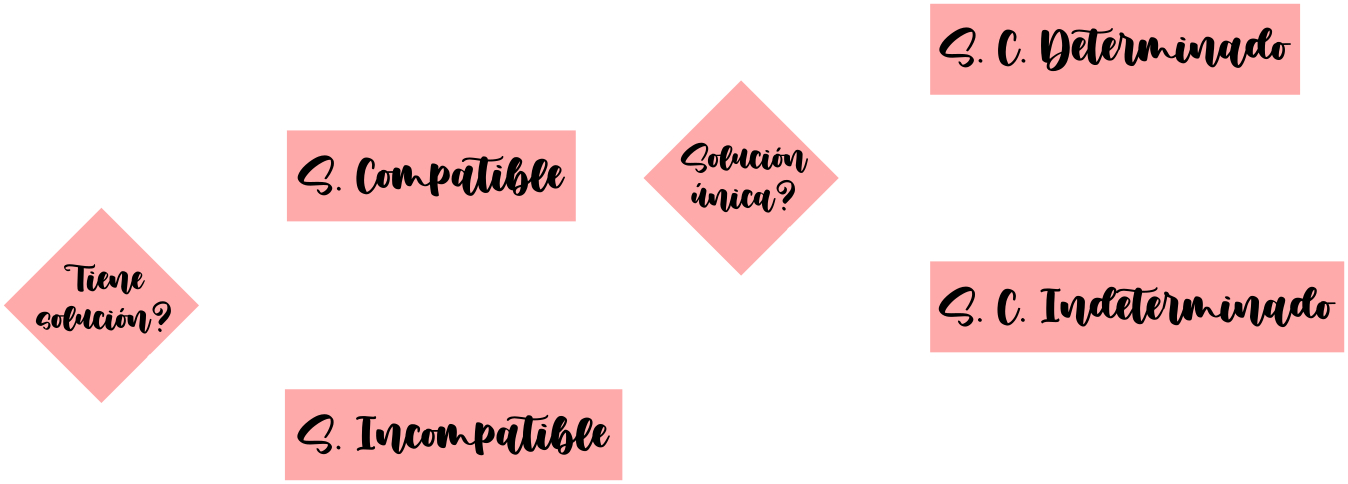
Métodos de resolución
- Substitución
- Igualación
- Reducción
3Resuelve los siguientes sistemas de ecuaciones indicando de que tipo de sistema se trata. Usa Todos los métodos:
- a \[ \begin{cases} x+5y = -1 \\ 3x-2y = 14 \end{cases} \]
- b \[ \begin{cases} 2x+3y = 21 \\ -x + y = 2 \end{cases} \]
- c \[ \begin{cases} 5x-3y = 41 \\ 4x + y = 26 \end{cases} \]
- d \[ \begin{cases} 2(x+3) - 4(x+2y-1) = 21 \\ 5(3x-y) + 3(2x+4y-2) = -6 \end{cases} \]
- e \[ \begin{cases} \frac{9(x-2)}{10} - \frac{4(2y + 3)}{15} = \frac{-7}{30} \\ -\frac{5(x+4)}{12} + \frac{7(y-1)}{18} = -\frac{1}{36} \end{cases} \]
- f \[ \begin{cases} \frac{3(x+1)}{2} - \frac{7(y-2)}{10} = \frac{4}{5} \\ \frac{3(x2-1)}{8} + \frac{5(y-2)}{6} = \frac{11}{24} \end{cases} \]
Sistemas de ecuaciones no lineales
Solución de un sistema de ecuaciones no lineal
Ver en GeogebraMétodos de resolución
Los mismos que en los lineales pero "con cuidado".
4Resuelve los siguientes sistemas de ecuaciones no lineales:
- a \[ \begin{cases} x^2 + y^2 = 2 \\ x + 2y = -1 \end{cases} \]
- b \[ \begin{cases} xy = -6 \\ 2x - y = 7 \end{cases} \]
- c \[ \begin{cases} 3x - 2y = -7 \\ x^2 + 3y^2 = 13 \end{cases} \]
- d \[ \begin{cases} x^3 - y^2 = 11 \\ x-y = -1 \end{cases} \]
- e \[ \begin{cases} xy^2 = 3 \\ 2x+5y=1 \end{cases} \]
- f \[ \begin{cases} \sqrt{x} + 2y = -4 \\ x+y = 1 \end{cases} \]
- g \[ \begin{cases} x - \sqrt{y+1} = 2 \\ 2x + 4y = 6 \end{cases} \]
- h \[ \begin{cases} \sqrt{x} + \sqrt{y} = 5 \\ 2x-y = -1 \end{cases} \]
- i \[ \begin{cases} \sqrt{x-1} + \sqrt{y} = 8 \\ -\sqrt{x+6} + 2\sqrt{y} = 6 \end{cases} \]
Sistemas de inecuaciones
Sistemas de inecuaciones de una incógnita
5Resuelve los siguientes sistemas de inecuaciones con una incógnita:
- a \[ \begin{cases} 2x + 3 \gt 7\\ 3x - 3 \lt 9 \end{cases} \]
- b \[ \begin{cases} x - 5 \ge -3 \\ 2x + 5 \lt 15 \end{cases} \]
- c \[ \begin{cases} 2(x+1) - 3(2x-3) \ge 5x +2\\ -(3x+4) + 2(x+2) \lt 3(2-x) - 2 \end{cases} \]
- a \[ \begin{cases} 3(2x-7) + 5(x-3) \lt 2(x-9)\\ 4(2x-5) - 3(4x-7) \le 6(x+1) + 5(x+2) \end{cases} \]
- b \[ \begin{cases} \frac{3x}{10} + \frac{2}{5} \gt \frac{x}{2} - 1 \\ \frac{5}{6} - \frac{7x}{9} \le \frac{2x}{3} - \frac{7}{2} \end{cases} \]
- f \[ \begin{cases} \frac{x}{12} - \frac{5x}{18} \le \frac{7}{6} \\ \frac{7x}{9} + \frac{x}{12} \le \frac{5x}{6} + \frac{1}{4} \end{cases} \]