Tema 3
Polinomios
Expresión algebraica
Una expresión algebraica es una combinación de letras, números y signos de operaciones.
Variables/incógnitas
Las letras
Valor numérico
Resultado de substituir una variable por un número en una expresión algebraica.
Enunciado: El doble de un número más uno
Expresión algebraica: \[ 2x + 1 \]
Valor númerico con si el número es 2: \[2 \cdot 2 + 1 = 5\]
Monomios
Expresión alxebraica formada por un producto de números e letras.
Partes de un monomio
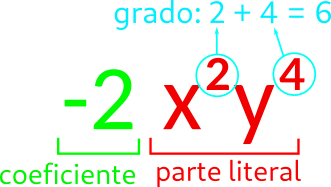
1Indica el coeficiente, parte literal y grado de los siguientes monomios:
- a \[ 3x^3y \]
- b \[ -7x^2yz \]
Monomios semejantes
Son aquellos que tiene la misma parte literal.
Operaciones: suma y resta
Solo podemos sumar/restar monomios semejantes.
Sumamos o restamos los coeficientes manteniendo la parte literal.
\[ 2x^2 + 5x^2 = 7x^2 \]
Operaciones: multiplicación y división
Podemos multiplicar/dividir cualquier par de monomios.
Multiplicamos o dividimos coeficiente y parte literal
\[ (2xy^2) \cdot (3 x^4y) = (2\cdot3)x^{1+4}y^{2+1} = 6x^5y^3\]
Operaciones: potenciación
Aplicamos la propiedad del producto de un producto y elevamos cada uno de los factores de un monomio.
\[ (2x^2y)^3 = 2^3 \cdot x^6 \cdot y^3 = 8x^6y^3 \]
2 Realiza las siguientes operaciones con monomios:
- a \[ 2x \cdot 3y + 4xy^2 : 2y^2 + 10xy \cdot 3 \]
- b \[ ((12x^2y)^2 \cdot 3x^2) : 2x^2 \]
- c \[ (3x^2)^3 - 4x^2 \cdot 3x + (4x^2)^2 \]
Polinomios
Partes de un polinomio
3 Indica cuales son los términos, el término independiente (si tiene) y el grado de los siguientes polinomios. Calcula su valor numérico para \[x=3\].
- a \[ -5x^3 + 3x^2 - 2 \]
- b \[ 5x + x^4 - 3 \]
Ops. con polinomios: suma, resta y producto por escalar
- \[(x^2 + 3) + (x^3 + 2x^2) = x^2 + 3 + x^3 + 2x^2 = \\ = x^3 + 3x^2 + 3\]
- \[(x^2 + 3) - (x^3 + 2x^2) = x^2 + 3 - x^3 -2x^2 = \\ = -x^3 -x^2 + 3\]
- \[2 \cdot (x^2 + 3) = 2x^2 + 6\]
4Dados los polinomios \[P(x)=\], \[Q(x)= \] y \[R(x) = \], calcula:
- a \[-2(x^4 - 2x^3 -x^2) - (3x^2 +6x - 4)\]
- d \[(3x^2 +6x - 4) + 2 \cdot (4x^3 + 5x - 2) - 3 \cdot (x^4 - 2x^3 -x^2)\]
\[(2a + 3b) \cdot (x + y + z) = \\ = 2a \cdot (x+ y + z) + 3b \cdot (x+ y + z)\]
5Resulve las siguientes multiplicaciones de polinomios:
- a \[(2x^2 - x + 5) \cdot (-x+3) \]
- b \[(-4x + 1) \cdot (2x^2 + 3x - 5) \]
- c \[(2x - 4) \cdot (3x^2 - 3x + 1) \]
Potencia de polinomios
\[ 2^3 = 2 \cdot 2 \cdot 2 \] \[ (x^2 + x)^3 = (x^2 + x) \cdot (x^2 + x) \cdot (x^2 + x) \]6Calcula las siguientes potencias de polinomios:
- a \[(x^2 + x + 3)^2 \]
- b \[(3x^2 + 2x + 5)^3 \]
Identidades notables
\[ (a + b)^2 = a^2 + 2ab + b^2 \] \[ (a - b)^2 = a^2 - 2ab + b^2 \] \[ (a + b) (a - b) = a^2 - b^2 \]7Calcula usando igualdades notables:
- a \[(x + 3)^2 \]
- b \[(x^3 - 3x)^2 \]
- c \[(x+4) \cdot (x-4) \]
- d \[(5xy + 4y) \cdot (5xy - 4y) \]
Potencias de un binomio
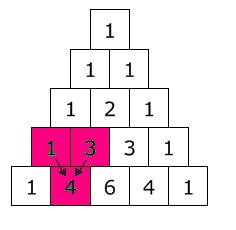
8Calcula las siguientes potencias de binomios:
- a \[ (3x + 2)^4 \]
- b \[ (2xy^2 +4x)^3 \]
- c \[ (x + 2)^5 \]
- d \[ (x^2y - 3x)^3 \]
- e \[ (x^3y^2 - 2x^2)^3 \]
Sacar factor común
\[ (2x) \cdot (3xy + 7x^2) = 6x^2y + 14x^3 \]
\[ 6x^2y + 14x^3 = (2x) \cdot (3xy + 7x^2) \]
9Saca factor común en los siguientes polinomios:
- a \[6x^4 + 12x^3 - 8 x^2 \]
- b \[-6x^3y - 9x^3y^2 + 15x^2y^2 - 3x^2y \]
- c \[x^3yz^2 + x^2y^3z^2 \]
- d \[-12ab^3c - 9b^3c^3 - 15b^2c^2d \]
- e \[2x^3yz - 3x^2y^2z + x^2yz^3 + x^2yz - x^4y^2z^2 \]
División de polinomios
10Realiza las siguientes divisiones de polinomios:
- a \[(3x^5 - 4x^3 + 2x - 3) : (x^2 + 2x - 3) \]
- b \[(6x^6 + 5x^5 - 3x^3 + 2x - 1) : (x^2 - 1) \]
- c \[(x^5 + 1) : (x^3 + x^2 + 2x - 5) \]
- d \[(3x^6 - 5x^5 + 4x^4 - 2x^3 + 3x^2 - x + 2) : (x^2 - x + 2) \]
Método de Ruffini
11Realiza las siguientes divisiones usando el método de Ruffini:
- a \[(3x^3 - 2x + 5) : (x-5) \]
- b \[(2x^6+4x^5-3x^4+8x^3+4x-9) : (x+3) \]
- c \[(x^5-3x^4-10x^2-22x-3) : (x -4) \]
- d \[5x^5-3x^4-9x^3+3x^2-16x-10) : (x - 2) \]
Factorización de un polinomio
12Factoriza los siguientes polinomios:
- a \[ x^3 + x^2\]
- b \[ 2x^3 + 3x^2 - 2x \]
- c \[ x^4 + 4x^3 - 5x^2\]
- d \[ x^4 - 25x^2\]
- e \[ x^4 - 4x^3 - 12x^2\]
- f \[ 7x^3 + 5x^2 - 2x\]
Raíces de un polinomio
Un valor o conjunto de valores es raíz de un polinomio cuando el valor numérico del polinomio con dichos valores es 0.
Teorema del Resto
13 Calcula las raíces de los siguientes polinomios:
- a \[ x^4 - 7x^3 -6x^2 + 72x\]
- b \[ x^4 - x^3 -25x^2 + 25x\]
- c \[ x^4 + x^3 - 36x^2 - 36x \]
- d \[ x^4 + x^3 -10x^2 + 8x \]
Fracciones algebraicas
Simplificación
14Simplifica las siguientes fracciones algebraicas:
- a \[ \frac{x^2 -9}{x^2-x-6} \]
- b \[ \frac{x^2 + 5x + 6}{2x^2 + 6x + 4} \]
- c \[ \frac{x^2 + 6x + 9}{2x^3 + 4x^2 - 6x} \]
Suma y resta de fracciones algebraicas
15Opera y simplifica si es posible:
- a \[ \frac{1}{x^2 - 3x - 4} - \frac{2}{x-4} + \frac{5}{x+1} \]
- b \[ \frac{x}{2x^2 +3x - 5} - \frac{1}{x-1} - \frac{x}{2x + 5} \]
- c \[ \frac{x+3}{x^2-5x+4} + \frac{2x}{x-4} + \frac{1}{x-1} \]
Multiplicaciones y divisiones
16Opera y simplifica si es posible:
- a \[ \frac{9x}{3x-3} \cdot \frac{x^2-1}{3x^2} \]
- b \[ \frac{x^2 - 25}{x^2 + 25} \cdot \frac{x+5}{x-5} \]
- c \[ \frac{x^2-1}{x^2 - 4x +4} : \frac{x^2 + 2x + 1}{x^2 - 4} \]
- d \[ \frac{2x-1}{x^2 + 2x} : \frac{4x}{x^3 + 2x^2} \]