UD1: Conjuntos numéricos. Porcentajes

Números decimales aproximación y errores

Aproximación de números decimales

Truncamiento
Redondeo

1 Aproxima los siguientes números según se indica:

a \[12,3476 \] redondeo a las milésimas 12,348
b \[ 2,288 \] truncamiento a las décimas 2,2
c \[ 3,272 \] redondeo a las centésimas 3,27
d \[ 2,345 \] truncamiento a las décimas 2,3

2 (pag. 22, ej. 69) Escribe un número con las siguientes características:

a Decimal periódico puro cuyo redondeo a las milésimas es 5,677 5,67676767... - 5,676676...
b Decimal periódico mixto cuyo truncamiento a las centésimas es 0,97 0,97777777777... - 0,972222222... - etc.
a Irracional cuyo redondeo a las diezmilésimas sea 0,0023 0,0023234238476283764...

Errores absoluto y relativo

\[E_a = |V_{estimado} - V_{real}| \]

\[E_r = \frac{E_a}{V_{real}} = \frac{|V_{estimado} - V_{real}|}{V_{real}} \]

3 (pag. 22, ej. 72 y 74) Calcula el error absoluto y el error relativo cometidos:

a Al considerar 3,5 como la longitud de un listón que mide realmente 3,59 cm. Ea=0.09 Er=0.025
b Al considerar 60m como la distancia entre dos postes situados a 59,91m. Ea=0,09 Er=0,0015
c Al aproximar 3,78496 por 3,7 Ea = 0,08496 Er=0,224
d Al aproximar \[\sqrt{7}\] por 2,65 Ea = 0,004248 Er=0,00160

Iniciación a la teoría de conjuntos

Definición de conjunto

No importa el orden.
No hay elementos repetidos.
Existen conjuntos finitos e infinitos.
Pueden ser continuos y discretos.
Definición por compresión y por expansión.

Notación

Los conjuntos se representan por letras mayusculas
Enumeramos entre llaves los miembros de un conjunto o su descripción.

4Da ejemplos de conjuntos que cumplan las siguientes propiedades. Defínelos tanto por compresión como por expansión.

a Un conjunto infinito y continuo. A = {"los números comprendidos entre 1 y 3"} A = {1, 1'1, 1'2, 1'3, 1'4...}
b Conjunto finito y discreto: B = {"los números pares positivos menores que 8"} B={2,4,6}

Operaciones con conjuntos

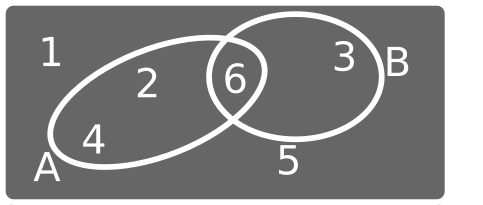
A = {"números pares"} y B = {"números multiplos de 3"}

Operaciones con conjuntos: la unión

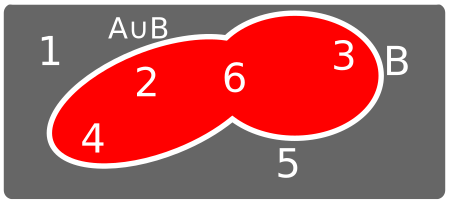
Operaciones con conjuntos: la intersección

5Sean los conjuntos A={"números naturales menores que 10"}; B = {"pares positivos menores que 15"} y C ="múltiplos de 3 positivos menores que 13" calcula:

a A U B = {1,2,3,4,5,6,7,8,9,10,12,14}
b A ∩ B = {2, 4, 6, 8, 10, 12, 14}
c A ∩ C = {3, 6, 9}
d B ∩ C = {6, 12}

Diagramas de Venn

6Representa los conjuntos del ejercicio 5 usando diagramas de Venn:

A = {"números naturales menores que 10"}
B = {"pares positivos menores que 15"}
C = {"múltiplos de 3 positivos menores que 13"}

Conjuntos numéricos

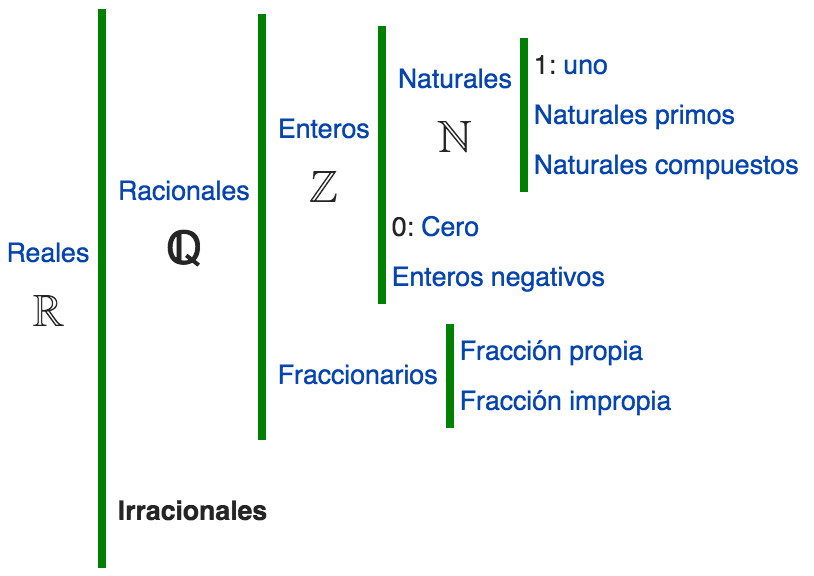
Notación

Representación de los conjuntos numéricos: \[\mathbb{N}, \mathbb{Z}, \mathbb{Q}, \mathbb{R}, \mathbb{I}\]
Símbolo para indicar pertenecia a un conjunto: \[2 \in \mathbb{N}\]

7 (pág 21. ej. 54) Clasifica los siguientes números en naturales, enteros, racionales o irracionales:

a 25,37 \[ \in \mathbb{Q} \]
b -6/17 \[ \in\mathbb{Q} \]
c 2/5 \[ \in \mathbb{Q} \]
d \[-\sqrt{12}\] \[ \in \mathbb{I} \]
e \[ \pi \] \[ \in \mathbb{I} \]
f 7/90 \[ \in \mathbb{Q} \]
g \[\sqrt{64}\] \[ \in \mathbb{N} \]
h -5 \[ \in \mathbb{Z} \]

8 (pág 21. ej. 55) Clasifica los siguientes números en naturales, enteros, racionales o irracionales:

a 2054,3 \[ \in \mathbb{Q} \]
b \[-27,3\hat{5}\] \[ \in \mathbb{Q} \]
c \[\sqrt{256}\] \[ \in \mathbb{N} \]
d \[\frac{\pi}{5}\] \[ \in \mathbb{I} \]
e -47 \[ \in \mathbb{Z} \]
f \[\sqrt{31}\] \[ \in \mathbb{I} \]

Intervalos

Definición de intervalo.

Extremos: abierto o cerrado

9Expresa mediante intervalos:

a Números reales del 3 al 9 incluyendo el 3 pero no el 9. [3, 9)
b Números reales del 2 al 5 incluyendo ambos extremos. [3, 5]
c Números reales entre el -3 y el 4 sin incluir ninguno de los dos extremos. \[ (-3, 4) \]

Semirectas

Notación: definimos intervalos por compresión

\[ \{x \in \mathbb{R} / -2 \lt x \le 9\} = (-2, 9] \]

10 (pag. 23 - ej. 81) Describe los siguientes intervalos:

a (0,7) \[= \{x \in \mathbb{R} / 0 \lt x \lt 7 \} \]
b [3,7) \[= \{x \in \mathbb{R} / 3 \le x \lt 7 \} \]
c [-2,4) \[= \{x \in \mathbb{R} / -2 \le x \lt 4 \} \]
d [-5,-3] \[= \{x \in \mathbb{R} / -5 \le x \le \} \]
e (-4,-2) \[= \{x \in \mathbb{R} / -4 \lt x \lt -2 \} \]
f [-7, -3) \[= \{x \in \mathbb{R} / -7 \le x \lt -3 \} \]
g [5,6) \[= \{x \in \mathbb{R} / 5 \le x \lt 6 \} \]
h [4, 6] \[= \{x \in \mathbb{R} / 4 \le x \le 6 \} \]

11 (pag. 23 - ej. 82) Describe los siguientes intervalos:

a \[\{x \in \mathbb{R} / -1 \le x \lt 5 \} \] = [-1, 5)
b \[\{x \in \mathbb{R} / -1 \ge x \gt -5 \} \] = (-5,-1]
c \[\{x \in \mathbb{R} / -3 \lt x \} \] \[= (-3, \infty) \]
d \[\{x \in \mathbb{R} / 3 \gt x \} \] \[= (-\infty, 3) \]
e \[\{x \in \mathbb{R} / -1 \le x \le 0 \} \] \[= [-1,0] \]
f \[\{x \in \mathbb{R} / 0 \gt x \gt -5 \} \] \[= (-5, 0) \]
g \[\{x \in \mathbb{R} / x \le -4 \} \] \[= (-\infty, -4] \} \]
h \[\{x \in \mathbb{R} / x \ge 5 \} \] \[= \{x \in \mathbb{R} / [5, \infty) \} \]

Operaciones con intervalos

Unión e intersección

12 (pag. 23; ej. 88) Halla la unión y la intersección de los siguientes intervalos:

a \[A = [1,5) \] y \[B = [0,3) \] \[\cup = [0, 5) ; \cap = [1,3) \]
b \[A = (-2,4]\] y \[B =(-1,2] \] \[\cup = (-2, 4] ; \cap = (-1, 2] \]
c \[A = (-5, -3) \] y \[B = [-3, 0) \] \[\cup = (-5, 0); \cap = \emptyset \]
d \[A = (-7,-2) \] y \[B = [-7, -6) \] \[\cup = [-7, -2); \cap =(-7, -6) \]
e \[A = (-1,0) \] y \[B = (0,1) \] \[\cup = (-1,0) \cup (0,1) ; \cap = \emptyset \]

f \[A = (-4, 2] \] y \[B = (2,3] \] \[\cup = (-4, 3] ; \cap = \emptyset \]
g \[A = (-\infty, 2] \] y \[B = (3,4) \] \[\cup = A \cup B ; \cap = \emptyset \]
h \[A = (-5, -1) \] y \[B = (-1, \infty) \] \[\cup = A\cup B ; \cap = \emptyset \]
i \[A = (-\infty, -3] \] y \[B = (0, \infty) \] \[\cup = A\cup B ; \cap = \emptyset \]
j \[A = (-\infty,0] \] y \[B = [-1, \infty) \] \[\cup = (-\infty, \infty) = \mathbb{R} ; \cap = [-1, 0] \]

Porcentajes

Cálculos de porcentajes

13Calcula la x en cada caso para los siguientes porcentajes:

a 30% de 2500 = x x = 750
b 25% de x = 30 x = 120
c x% de 250 = 100 x = 40
d 5% de x = 45 x = 900

14 (pag. 24 - ej. 95) En una encuesta en la que las respuestas son SI, NO y NS/NC han participado 860 personas. Sabiendo que 301 han contestado SI y 172 han respondido NO, ¿qué porcentaje corresponde a NS/NC?

El 45% corresponde a NS/NC.

15 (pag. 24 - ej. 96)El 56% de una cantidad es 2464, ¿cuál es la cantidad?

La cantidad es 4400.

Aumentos y disminuciones porcentuales

16¿Cuál es la cantidad final que se obtiene en cada uno de los procesos que se detallan a continuación partiendo de una cantidad inicial de 1200? (pag. 24 - ej. 101)

a Se experimenta un aumento del 20.5%. 1446
b Se experimenta una disminución del 35%. 780
c Se experimenta un aumento del 75%. 2100
d Se experimenta una disminución del 15.75%. 1011

17 (pag. 24 - ej. 102)¿Cuál es la cantidad inicial de la que se ha partido en cada uno de los procesos que se detallan a continuación suponiendo que la cantidad final es 240?

a Se experimenta un aumento del 32%. 181.818
b Se experimenta un disminución del 2'4%. 245'901
c Se experimenta un aumento del 16'8%. 205.479
d Se experimenta un disminución del 48%. 461.538

Porcentajes encadenados

18 (pag. 24 - ej. 108) Un comercial sube un 30% el precio de sus artículos cuando los pone a las venta y luego hace un 15% de descuenteo. ¿Qué precio tendrá un artículo si le costón 45€ ¿A qué porcentaje del precio inicial corresponde?

19 (pag. 24 - ej. 109) ¿Cuanto valía un producto que despues de dos descuentos, uno edl 25% y otro del 30%, vale 125€?

20 (pag. 24 - ej. 110) ¿Cuál era el precio de un abrigo que está etiquetado en 120€, sabiendo que se ha añadido un 21% de IVA y que se obtiene una ganancia del 18%?

21 (pag. 24 - ej. 111) ¿Aplicar a una cantidad dos aumentos del 25%, uno tras otro, es lo mismo que aplicar un aumento del 25% al doble de la cantidad?

Interés simple

22 (pag. 24 - ej. 115) Calcula el interés que se obtiene al depositar 20000€ en una entidad bancaria durante 4 años, al 2.75% de rédito anual.

23 (pag. 25 - ej. 119) Laura pide un préstamo de 4000€ y devuelve 5080€ en un pago único con intereses al cabo de 3 años. Dabiendo que es un interés simple calcula el rédito del préstamo.