Tema 2: Potencias y radicales
Definición de potencia
\[ 2^4 = 2 \cdot 2 \cdot 2 \cdot 2 \]
\[ 2^1 = 2 \] \[ 2^0 = 1 \]
Potencia de exponente negativo
\[ a^{-n} = \frac{1}{a^n} \]
\[ 2^{-1} = \frac{1}{2} \]
\[ 2^{-3} = \frac{1}{2^3} = \frac{1}{8} \]
Operaciones con potencias
\[ a^p \cdot a^q = a^{p+q} \]
\[ a^p : a^q = a^{p-q} \]
\[(a \cdot b)^p = a^p \cdot b^p\]
\[(\frac{a}{b})^p = (a : b)^p = a^p : b^p = \frac{a^p}{b^p} \]
\[ (a^p)^q = a^{p \cdot q} \]
1 Realiza las siguientes operaciones con potencias (cont.):
- a \[ 2^3 \cdot 2^4\] \[ = 2^7 \]
- b \[ 2^3 \cdot 2^4 \cdot 2^5\] \[ = 2^{12} \]
- c \[ 3^1 \cdot 3^5 \cdot 3^{-2} \] \[ = 3^4 \]
- d \[ 3^2 \cdot 3^{-2} \] \[ = 3^0 = 1 \]
- e \[ 7^3 : 7^2 \] \[ = 7^1 = 7 \]
- f \[ 7^3 : 7 \] \[ = 7^2 \]
- g \[ 7^3 : 7^{-4} \] \[ = 7^7 \]
1 Realiza las siguientes operaciones con potencias (cont.):
- h \[ \frac{7^3}{7^2} \] \[ = 7^1 = 7 \]
- i \[ \frac{7^3}{7^{-5}} \] \[ = 7^8 \]
- j \[ (2^3)^7 \] \[ = 2^{21} \]
- k \[ (2^{-4})^2 \] \[ = 2^{-8} \]
- l \[ ((2^3)^5)^{-2} \] \[ = 2^{-30} \]
- m \[ (2 \cdot 3)^3 \] \[ = 2^3 \cdot 3^3 \]
- n \[ (2 \cdot 3)^3 \cdot 2^2 \] \[ = 2^5 \cdot 3^3 \]
1 Realiza las siguientes operaciones con potencias (cont.):
- ñ \[ (2 \cdot 7)^3 \cdot 2^3 \cdot 5^2 \cdot 7 \] \[ = 2^6 \cdot 5^2 \cdot 7^4 \]
- o \[ (2 \cdot 7)^3 \cdot (3 \cdot 7)^4 \] \[ = 2^3 \cdot 3^4 \cdot 7^7 \]
- p \[ (2^2 \cdot 7)^3 \cdot 7^4 \] \[ = 2^6 \cdot 7^7 \]
- q \[ (3^4 \cdot 5)^4 \cdot (2 \cdot 5^2)^3 \] \[ =2^3 \cdot 3^{16} \cdot 5^{10} \]
1 Realiza las siguientes operaciones con potencias (cont.):
- r \[ (12)^2 \cdot 2^3 = (2^2 \cdot 3)^2 \cdot 2^3 \] \[ = 2^7 \cdot 3^2 \]
- s \[ 12^3 \cdot 63^2 \]
- t \[ 24^2 \cdot 8^3 \cdot 10^2 \]
- u \[ 40^2 \cdot (15)^3 \]
1 Realiza las siguientes operaciones con potencias (cont.):
- v \[ \frac{2^3 \cdot 3^2 \cdot 5^3}{3^4 \cdot 5^6 \cdot 2^5} \]
- w \[ \frac{12^2 \cdot 15^3}{16 \cdot 25^2 \cdot 9} \]
- x \[ \frac{36^2 \cdot 25}{15 \cdot 8^3} \]
- y \[ \frac{12 \cdot 90^3}{40^4 \cdot 16} \]
1 Realiza las siguientes operaciones con potencias (cont.):
- z \[ \frac{(-2)^3 \cdot 12^2}{(-3)^2} = \]
- a2 \[ \frac{(-2)^3 \cdot 3^2 \cdot (-5)^3}{(-3)^5 \cdot 2^7} = \]
- b2 \[ \frac{11^3 \cdot (-15)^6 \cdot 10}{21^3 \cdot (-25)^2} = \]
- c2 \[ \frac{(-30)^2 \cdot 5^2 \cdot 27^3}{3^5 \cdot (-25)^5} = \]
Notación científica

2 Escribe los siguientes números en notación científica:
- a \[ 567000000 \]
- b \[ 842300000000 \]
- c \[ 493000000 \]
- d \[ 0,0000040435 \]
- e \[ 0,003000234 \]
- f \[ 0,00000032453 \]
2 Escribe los siguientes números en notación científica (cont.):
- g \[ 0.0567 \cdot 10^3 \]
- h \[ 84.324 \cdot 10^{-4} \]
- i \[ 67 \cdot 10^3 \]
Lunes, 4 de noviembre
Operaciones con números en notación científica
Mismo exponente
\[ 3 \cdot 10^2 + 2 \cdot 10^2 \] \[= 300 + 200 \]
\[ = 5 \cdot 10^2\] \[= 500 \]
\[ 3 \cdot 10^2 + 2 \cdot 10^1 \] \[= 300 + 20 \]
\[ = 30 \cdot 10^1 + 2 \cdot 10^1 = \]
\[ = 32 \cdot 10^1 = 3.2 \cdot 10^2\]
3 Calcula el número que colocar en los siguientes huecos:
- a \[ 6.342 \cdot 10^4 \] = _____ \[ \cdot 10^2 \]
- b \[ 8.452 \cdot 10^{-2} \]= _____ \[ \cdot 10^1 \]
- c \[ 3.43 \cdot 10^{-3} \]= _____ \[ \cdot 10^2 \]
- d \[ 4.234 \cdot 10^5 \]= _____ \[ \cdot 10^3 \]
4 Realiza las siguientes operaciones con números en notación científica:
- a \[ 6.342 \cdot 10^4 + 5.34 \cdot 10^{-1} \]
- b \[ 8.452 \cdot 10^{-6} - 7.24 \cdot 10^{-8} \]
- c \[ 3.43 \cdot 10^3 + 2.45 \cdot 10^{-2} \]
- d \[ 4.234 \cdot 10^7 - 3.45 \cdot 10^5 \]
Miércoles, 6 de noviembre
5 Realiza las siguientes operaciones con números en notación científica:
- e \[ 6.342 \cdot 10^4 \cdot 5.34 \cdot 10^{-1} \]
- f \[ 8.452 \cdot 10^{-6} \cdot 7.24 \cdot 10^{-8} \]
- g \[ 3.43 \cdot 10^3 : 2.45 \cdot 10^{-2} \]
- h \[ 4.234 \cdot 10^7 : 3.45 \cdot 10^5 \]
Operaciones con fracciones con la calculadora
Fracciones propias/impropias - Número mixto
Propia) \[ \frac{2}{5} \]
Impropia) \[ \frac{4}{3} \]
Número mixto) \[ 1 + \frac{1}{3} \]

R1 Realiza las siguientes operaciones con fracciones usando la calculadora:
- a \[ \frac{2}{5} + \frac{1}{2} \cdot \frac{4}{3} - \frac{1}{6} \]
- b \[ \frac{3}{2} - \frac{4}{5} \cdot \frac{5}{6} \]
- c \[ (\frac{3}{2} - \frac{4}{5}) \cdot \frac{5}{6} \]
- d \[ \frac{7}{2} + \frac{1}{5} \cdot \frac{5}{6} \]
Jueves, 8 de noviembre
Raíces
\[ \sqrt[n]{a} = b \iff b^n = a \]
\[ \sqrt{9} = 3 \iff 3^2 = 9 \]
\[ \sqrt[3]{8} = 2 \iff 2^3 = 8 \]
...
6 Calcula sin usar la calculadora:
- a \[ \sqrt{9} \]
- b \[ \sqrt{25} \]
- c \[ \sqrt{49} \]
- d \[ \sqrt{0} \]
- e \[ \sqrt{1} \]
- f \[ \sqrt{0.25} \]
- g \[ \sqrt[4]{16}\]
- h \[ \sqrt[3]{8}\]
- i \[ \sqrt[3]{27}\]
Propiedades
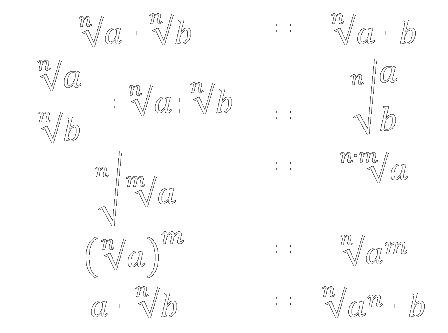
7 Simplifica las siguientes expresiones usando las propiedades de las raíces:
- a \[ 3\sqrt{7} + 4 \sqrt{7} - \sqrt{7} \]
- b \[ 4\sqrt[3]{10} \cdot 3 \sqrt[3]{2} \]
- c \[ 8 \sqrt[3]{9} : 2 \sqrt[3]{3} \]
- c \[ \sqrt[3]{\sqrt{4}} \]
Extraer factores de raíces
\[ \sqrt[3]{2^7 \cdot 3^6} = 2^2 \cdot 3^2 \cdot \sqrt[3]{2^1\cdot 3^0} \]8 Extraer factores:
- a \[ \sqrt{2^3} \]
- b \[ \sqrt{2^3 \cdot 7^4} \]
- c \[ \sqrt[3]{2^3 \cdot 5^7} \]
- d \[ \sqrt[3]{80} \]
- e \[ \sqrt[3]{200} \]
- f \[ \sqrt[4]{2500} \]
9 Extrae factores y suma donde sea posible:
- a \[ 2 \sqrt{8} + 5 \sqrt{72} − 7 \sqrt{18} - \sqrt{50} \]
- b \[ 3 \sqrt[3]{54} - 2 \sqrt[3]{250} + 4 \sqrt[3]{16} \]
Aproximación de números
10 Aproxima los siguientes números por redondeo y truncamiento:
- a \[ 9.876 \] (décimas)
- b \[ 0.973 \] (centésimas)
- c \[ 2.497 \] (unidades)
Errores absoluto y relativo
\[E_a = |V_{estimado} - V_{real}| \]
\[E_r = \frac{E_a}{V_{real}} = \frac{|V_{estimado} - V_{real}|}{V_{real}} \]
11 Calcula el error absoluto y relativo cometido:
- a Al aproximar \[ 9.876 \] con \[ 9.9 \]
- b Al aproximar \[ 9.876 \] con \[ 9.8 \]
- c Al aproximar \[ 9.973 \] con \[ 9.97 \]