Probabilidad
Experimentos y sucesos
Experimentos deterministas y aleatorios
Un experimento determinista es aquel en el que siempre se obtiene el mismo resultado al realizarlo bajo las mismas condiciones, mientras que en un experimento aleatorio el resultado puede variar.
Ejemplos: lanzar una moneda es un experimento aleatorio, mientras que medir la longitud de un objeto es determinista.
1Clasifica los siguientes experimentos en aleatorios o deterministas.
- Extraer una carta de una baraja.
- Pesar un litro de mercurio.
- Preguntar a tus compañeros un número.
- Lanzar tres monedas y anotar el número de caras.
- Medir la hipotenusa en un triángulo rectángulo de catetos 3cm y 4 cm.
2 En una bolsa hay 10 bolas de 3 colores diferentes. Escribe un experimento aleatorio y otro determinista.
Espacio muestral y sucesos
Sucesos elementales y espacio muestral
El espacio muestral es el conjunto de todos los resultados posibles de un experimento aleatorio. Un suceso elemental es un solo resultado dentro de ese espacio muestral.
Por ejemplo, al lanzar un dado, el espacio muestral es \( \Omega = \{1, 2, 3, 4, 5, 6\} \).
4 Escribe el espacio muestral de los siguientes experimentos aleatorios.
- Extraer una carta de la baraja española.
- Lanzar una chincheta y anotar la posición de caída.
- Sacar una bola de una urna con 5 bolas rojas, 3 azules y 2 verdes.
Sucesos compuestos
Un suceso compuesto es aquel que se forma combinando varios sucesos elementales.
Por ejemplo, en el lanzamiento de un dado, el suceso \(A = \text{"sacar un número par"}\) es compuesto, ya que incluye los resultados \(A = \{2, 4, 6\}\).
6 Se lanzan 2 dados y se multiplica el número de puntos obtenido en cada uno. ¿Cuántos resultados se pueden obtener? Describe el espacio muestral e indica dos sucesos que no sean elementales.
Sucesos seguro y imposible
El suceso seguro es aquel que siempre ocurre, como "sacar un número entre 1 y 6" al lanzar un dado. El suceso imposible es el que nunca ocurre, como "sacar un 7" en un dado de seis caras.
10 En una urna hay 5 bolas blancas y 4 bolas rojas. Describe un suceso seguro y uno imposible.
Operaciones con sucesos
Operaciones con sucesos: unión
La unión de dos sucesos incluye todos los resultados que pertenecen a al menos uno de los sucesos.
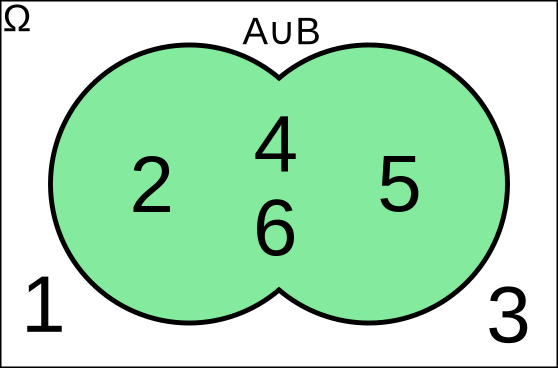
Si \(A\) es "sacar un número par" y \(B\) es "sacar un número mayor que 3", la unión \(A \cup B = \{2, 4, 5, 6\}\).
Operaciones con sucesos: intersección
La intersección de dos sucesos incluye solo los resultados comunes.
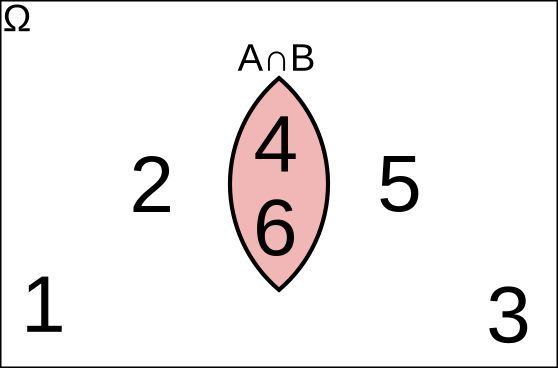
Si A es "sacar un número par" y B es "sacar un número mayor que 3", la intersección \(A \cap B = \{4, 6\}\)
Espacio Muestral (\(\Omega\)): lanzar un dado
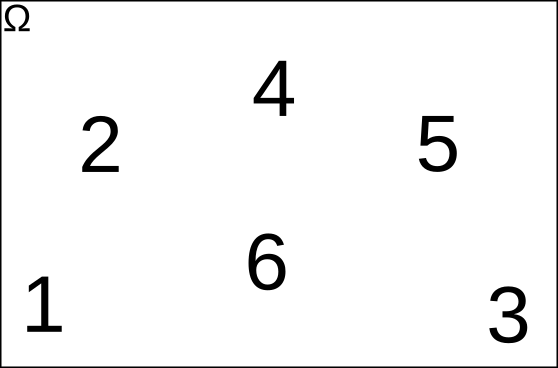
Suceso \(A = \) "sacar un número par"
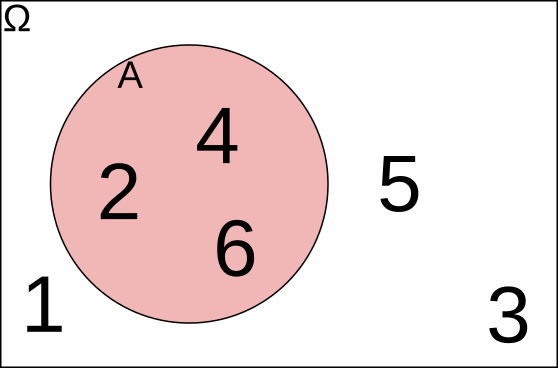
Suceso \(B = \) "sacar un número mayor que 3"
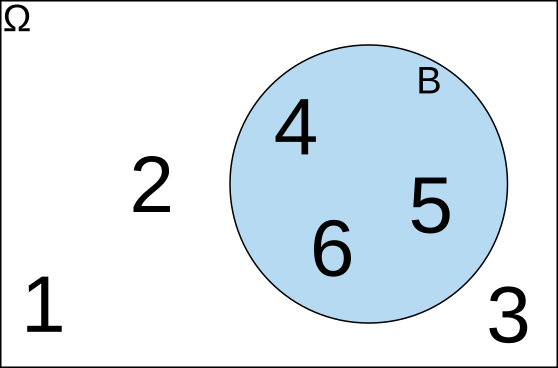
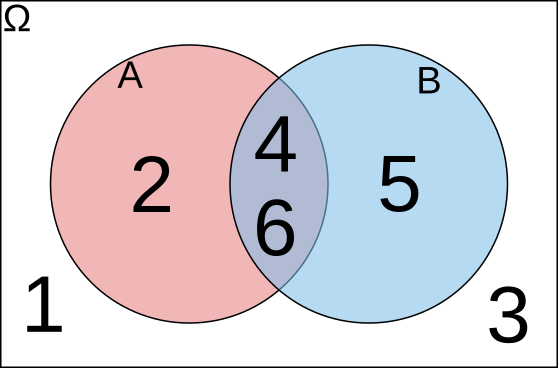
Unión \(A \cup B\)
Intersección \(A \cap B\)
13 Calcula la unión y la intersección de los sucesos $A = \{1, 2, 3\}$ y $B = \{1, 3, 5\}$. Represéntalo con un diagrama de Venn:
14 Extraemos una carta de la baraja. Halla la unión y la intersección de las siguientes parejas de sucesos.
- A = «Sacar oros» y B = «Sacar copas».
- C = «Sacar as» y D = «No sacar as».
- F = «Sacar bastos» y G = «Sacar as».
15 Al extraer una carta de la baraja española expresa en forma de uniones e intersecciones los siguientes sucesos.
- «Que salga un número menor que 5 y mayor que 2».
- «Que salga una figura y sea de bastos».
- «Que no salga un as».
Sucesos incompatibles
Dos sucesos son incompatibles si no pueden ocurrir al mismo tiempo y por lo tanto su intersección es nula.
Por ejemplo, en el lanzamiento de un dado, "sacar un 1" y "sacar numero par" son incompatibles.
18 Determina dos sucesos compatibles y otros dos incompatibles en el experimento aleatorio de lanzar dos monedas al aire.
19En un bombo hay 15 bolas numeradas del 1 al 15 y se extrae una de ellas. Escribe los elementos que forman los sucesos siguientes:
- A = "Múltiplo de 3"
- B = "Múltiplo de 2"
- C = "Mayor que 4"
Indica además un sucesos compatible y uno incompatible con cada uno de ellos.
Operaciones con sucesos: complementario
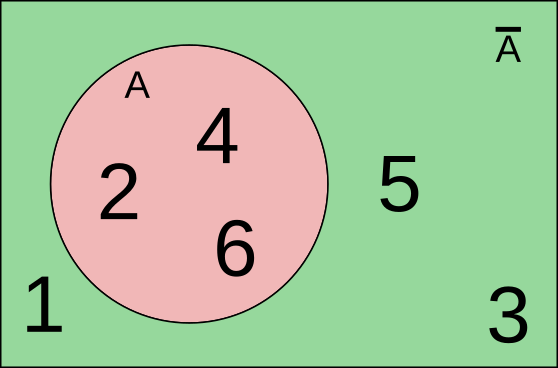
El complementario de un suceso A es el conjunto de resultados que no están en A.
Por ejemplo, si \(A\) es "sacar un número par", el complemento es \(\overline{A}\) = "sacar un número impar".

20 Considera el lanzamiento de 3 monedas. Escribe los siguientes sucesos: A = «Obtener al menos una cara» y B = «Obtener una sola cara». Calcula.
- $A \cup B$
- $A \cap B$
- $\overline{A}$
- $\overline{B}$
25Al lanzar un dado de 6 caras, $A = \{2, 4\}$ y $B = \{1, 2, 3\}$. Calcula:
- Calcula $A \cap B$
- Calcula $A \cup B$
- ¿Son A y B sucesos compatibles?
- Obtén el contrario de los sucesos $A$, $B$, $A \cap B$ y $A \cup B$.
Iniciación a la combinatoria
Técnicas para contar: diagrama de árbol
Un diagrama de árbol es una herramienta visual que ayuda a representar todas las posibles combinaciones de un experimento secuencial. Por ejemplo, al lanzar una moneda y luego un dado, cada rama representa un resultado posible.
27 Lanzamos una moneda y un dado de 6 caras. ¿Cuál es el espacio muestral? Ayudate de un diagrama de árbol.
Regla del producto
La regla del producto establece que si un experimento se compone de dos etapas, donde la primera tiene n resultados posibles y la segunda m resultados, el total de resultados es n × m.
Permutaciones
Las permutaciones son ordenamientos de un conjunto de $n$ elementos.
Por ejemplo, si queremos ordenar 3 letras A, B y C lo podemos hacer de 6 forma: ABC, ACB, BAC, BCA, CAB y CBA.
Permutaciones
¿Cuántas permutaciones (ordenaciones) podríamos hacer con un alfabeto de 5 letras? ¿Y con uno de 26?
\(P(n) = n!\)
Variaciones sin repetición
Las variaciones son cadenas ordenadas de elemento de dentro de un conjunto. En este caso como son sin repetición no podemos repetir los elementos del conjunto.
Por ejemplo, si queremos elegir dos letras de entre las letras {A, B, C} sin repetir podríamos hacerlo de 6 formas: AB, AC, BA, BC, CA y CB.
Variaciones sin repetición
¿Cuántas variaciones sin repetición podremos hacer con un alfabeto de 10 elementos si queremos elegir 4 letras?
\(V(n,m) = \frac{n!}{(n-m)!}\)
Variaciones sin repetición
Las variaciones son cadenas ordenadas de elemento de dentro de un conjunto. En este caso como son con repetición podemos repetir los elementos del conjunto.
Por ejemplo, si queremos elegir dos letras de entre las letras {A, B, C} sin repetir podríamos hacerlo de 9 formas: AB, AA, AC, BA, BB, BC, CA, CB y CC.
Variaciones sin repetición
¿Cuántas variaciones con repetición podremos hacer con un alfabeto de 10 elementos si queremos elegir 4 letras?
\(VR(n,m) = n^m\)
29 Dada una clase de 30 alumnos calcula:
- Número de formas de colocarlos en una fila ordenada.
- Número de formas de elegir un delegado y un subdelegado (teniendo en cuenta que no pueden ser la misma persona)
30 La contraseña de una determinada web tiene que tener 5 letras minúsculas elegidas del alfabeto (26 letras). Calcula lo siguiente:
- El número total de maneras en que se puede formar la contraseña si todas las letras deben ser distintas.
- El número de formas de formar la contraseña si se permite repetir letras.
Probabilidad
¿Qué es la probabilidad?
La probabilidad es una medida de la certidumbre de que un proceso ocurra. Es una cantida entre 0 (suceso imposible) y 1 (suceso seguro).
Ley de Laplace
En experimentos aleatorios simples y equiprobables, la probabilidad de un suceso es:
\(P(A) = \frac{\text{casos favorables}}{\text{casos posibles}}\)
Por ejemplo, si el experimento es lanzar dos monedas.
\( \Omega = \{CC, C+, +C, ++\}\)
\(A = \text{"sacar el mismo lado"} = \{CC, ++\}\)
\(P(\text{"sacar el mismo lado"}) = \frac{2}{4} \)
35Al lanzar un dado, calcula la probabilidad de obtener:
- Múltiplo de 5
- Divisor de 2
- Número primo
- Número 3
36 De una baraja española extraemos una carta.
- ¿Cuál es la probabilidad de sacar un caballo?
- ¿Y una figura?
- ¿Y oros?
- ¿Y una sota que no sea de copas?
37 En una caja hay 5 bolas amarillas y 7 bolas rojas.
- ¿Cuál es la probabilidad de sacar una bola amarilla?
- ¿Y una bola roja?
43 Con las letras de la palabra TECLA...
- ¿Cuántas posibles ordenaciones podríamos hacer de esas letras?
- ¿Seleccionada una de esas ordenaciones al azar, cual es la probabilidad de que empiece por la letra T?
- ¿Y, que termine por las letras LA?
44En la clase de Jaimito hay 30 alumnnos...
- ¿Cuántas son las posibles formas de escoger delegado y subdelegado?
- ¿Cuál es la probabilidad de que Jaimito salga elegido delegado o subdelegado?
- ¿Cuál es la probabilidad de que Jaimito no salga elegido ni delegado ni subdelegado?
Probabilidad: sucesos compuestos
Probabilidad de sucesos compuestos: diagrama de árbol
Podemos completar un diagrama de árbol añadiendole las probabilidades en las ramas de forma que la probabilidad de la intersección consiste en multiplicar el cambino.
Por ejemplo: Si tenemos una urna con 2 bolas rojas y 3 azules. Sacamos 2 bolas sin reemplazamiento...
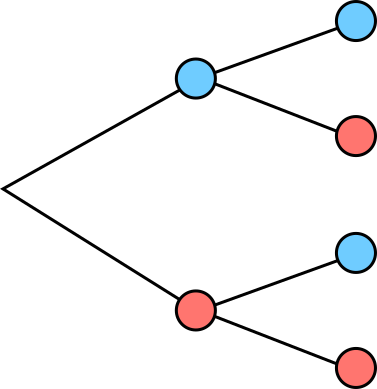
Si queremos calcular la probabilidad de sacar 2 bolas rojas...
46 Tenemos una bolsa que contiene 3 bolas blancas y 5 negras. Calcula la probabilidad de los siguientes sucesos:
- Extraer una bola y que sea blanca.
- Extraer una bola y que sea blanca y luego extraer una bola y que vuelva a ser blanca.
- Extraer una bola y que sea blanca, devolverla a la bolsa y luego extraer otra bola y que vuelva a ser blanca.
- Extraer una bola y que sea negra y luego extraer otra bola y que sea blanca.
48 Tenemos dos dados de 6 caras. Calcula las siguientes probabilidades.
- Lanzar un dado y que salga par.
- Lanzar un dado y que salga par y luego lanzar otro y que salga impar.
- Lanzar un dado y que salga un múltiplo de 3 y luego lanzar otro y que salga un 5
49 Tenemos dos bolsas con bolas rojas y verdes. Si lanzamos una moneda y sacamos cara, abrimos la bolsa A que contiene 4 bolas rojas y 2 verdes. Si sale cruz abrimos al bolsa B que contiene 2 bolas rojas y 3 verdes. Calcula las siguientes probabilidades:
- Calcula la probabilidad de sacar cara y una bola roja.
- ¿Cuál sería la probabilidad de sacar cruz y extraer las dos bolas rojas de forma consecuiva (sin reemplazamiento).
- ¿Cuál sería la probabilidad de sacar una bola roja?
- Sabemos que ha salido cara. ¿Cuál es la probabilidad de sacar una bola roja?
Probabilidad de sucesos compuestos: tabla de contingencia
Una tabla de contingencia es una forma de organizar los datos que nos ayuda a calcular las probabilidades de sucesos compuestos.
Por ejemplo, la siguiente tabla nos indica la relación entre el género y la mano dominane.
| Diestro | Zurdo | TOTAL | |
|---|---|---|---|
| Hombre | 43 | 9 | 52 |
| Mujer | 44 | 4 | 48 |
| TOTAL | 87 | 13 | 100 |
Con esos datos podemos calcular diversas probabilidades.
53Se sortea un viaje a Roma entre los 120 mejores clientes de una agencia de automóviles. De ellos, 65 son mujeres, 80 están casados y 45 son mujeres casadas. Se pide:
- ¿Cuál será la probabilidad de que le toque el viaje a un hombre soltero?
- Si del afortunado se sabe que es casado, ¿cuál será la probabilidad de que sea una mujer?
- Si del afortunado se sabe que es casado, ¿cuál será la probabilidad de que sea una mujer?
- ¿Cuál es la probabilidad de que sea Mujer?
54 En un viaje organizado por Europa para 120 personas, 48 de los que van saben hablar Inglés, 36 saben hablar Francés y 12 de ellos hablan los dos idiomas. Escogemos uno de los viajeros al azar.
- ¿Cuál es la probabilidad de que hable alguno de los dos idiomas?
- ¿Cuál es la probabilidad de que hable Francés, sabiendo que habla Inglés?
- ¿Cuál es la probabilidad de que solo hable Francés?
55 En una clase de 30 alumnos hay 18 que han aprobado Matemáticas, 16 que han aprobado Inglés y 6 que no han aprobado ninguna de las dos. Elegimos al azar un alumno de esa clase.
- ¿Cuál es la probabilidad de que se haya aprobado Inglés y Matemáticas?
- Sabiendo que ha aprobado Matemáticas, ¿cuál es la probabilidad de que haya aprobado Inglés?
Probabilidad: sucesos no equiprobables
Ley de los grandes números
La ley de los grandes números establece que, al repetir un experimento muchas veces, la frecuencia relativa de un suceso tiende a estabilizarse en torno a su probabilidad real.
59 Al lanzar una chincheta, puede caer con la punta hacia arriba o hacia abajo.
- ¿Son estos sucesos equiprobables?
- Para comprobar la pregunta anterior, realiza el experimento 100 veces: ¿Es mayor la frecuencia relativa del suceso «Punta hacia arriba»? Compara tu resultado con el obtenido por tus compañeros y formad una tabla juntando todos los resultados.
60 Se lanza un dado de 4 caras y se anotan las veces que no aparece la cara 1. A continuación se muestra la tabla de frecuencias:
| Lanzamientos | 20 | 40 | 60 | 80 | 100 |
|---|---|---|---|---|---|
| fi | 7 | 11 | 15 | 18 | 27 |
- Obtén la tabla de frecuencias relativas.
- ¿Hacia qué valor tiende?
- ¿Qué probabilidad le asignarías?