Estadística
Estudio estadístico: conceptos
El estudio estadístico es el proceso mediante el cual se recogen, organizan y analizan datos para obtener conclusiones. Los estudios pueden realizarse sobre toda una población o una muestra de ella.
Población y muestra
La población es el conjunto total de elementos sobre los que se realiza el estudio. La muestra es un subconjunto de la población que se selecciona para ser estudiada. Los resultados obtenidos de la muestra se utilizan para hacer inferencias sobre toda la población.
1 Queremos realizar un estudio estadístico de la talla de calzado que usan los alumnos de 3ºESO de un instituto.
- ¿Cuál sería la población?
- Elige una muestra. ¿Qué tamaño tiene?
2 Señala en qué caso es más conveniente estudiar la población o una muestra.
- La longitud de los tornillos que, ininterrumpidamente, produce una máquina.
- La estatura de todos los turistas en un año.
- El peso de un grupo de cinco amigos.
3 Este es el titular de un periódico. «EL PESO MEDIO DE LOS ESPAÑOLES ES 69 KG.»
- ¿Cómo crees que se llega a esta conclusión? ¿Se habrá estudiado a toda la población?
- ¿Qué características debe tener la muestra? ¿Podrían ser todos los individuos de la muestra de la misma edad? Si todos son mujeres, ¿sería correcta la muestra?
Variables estadísticas
Variables estadísticas
Las variables estadísticas son las características o cualidades que se estudian en una población. Pueden ser cualitativas o cuantitativas, dependiendo de si representan atributos o cantidades.
Tipos de variables estadísticas
Las variables cuantitativas pueden ser discretas (valores enteros, como el número de hermanos) o continuas (pueden tomar cualquier valor dentro de un rango, como la altura). Las cualitativas pueden ser ordinales (con un orden) o nominales (sin orden).
5 Indica si las siguientes variables estadísticas son cualitativas o cuantitativas:
- Comida Favorita.
- Profesión que te gusta.
- Número de goles marcados por tu equipo.
- Número de alumnos de tu Instituto.
6 De las siguientes variables cuantitativas, indica cuáles son discretas y cuáles continuas:
- Número de hijos de 50 familias.
- Temperaturas registradas en Casablanca.
- Duración de un automóvil.
- Número de acciones vendidas en la Bolsa.
7 Clasifica las siguientes variables en cualitativas y cuantitativas discretas o continuas:
- La nacionalidad de una persona.
- Litros de agua contenidos en un depósito.
- Número de libros en un estante de librería.
- Puntos al lanzar dos dados.
Tabla de frecuencias
Frecuencias absoluta y frecuencia absoluta acumulada
La frecuencia absoluta es el número de veces que aparece un valor en un conjunto de datos. La frecuencia absoluta acumulada es la suma de las frecuencias absolutas hasta un valor determinado.
Frecuencia relativa y frecuencia relativa acumulada
La frecuencia relativa es el cociente entre la frecuencia absoluta de un valor y el total de datos. La frecuencia relativa acumulada es la suma de las frecuencias relativas hasta un valor determinado.
8 El color de pelo (M = moreno, R = rubio, P = pelirrojo) de 30 personas es:
M R P M M M M R R P P M M M M M M P R R R P M M M M R M M M
Construye su tabla de frecuencias.
9 El número de horas diarias que trabajan con el ordenador 30 personas es:
3 4 0 5 5 3 4 5 0 2 2 5 3 2 0 1 2 2 1 2 0 3 1 2 1 1 2 1 4 3
- ¿De qué tipo es la variable estadística?
- Construye la tabla de frecuencias.
Variables continuas: clases y marcas de clase
Cuando las variables son continuas, es común agrupar los datos en clases o intervalos. La marca de clase es el punto medio de cada intervalo y se utiliza para representar el valor promedio de los datos en ese intervalo.
14 Los resultados de un test de inteligencia realizado a 20 personas han sido:
100 80 92 101 65 72 121 68 75 93 101 100 102 97 89 73 121 114 113 94
Obtén la tabla de frecuencias, tomando intervalos de amplitud 10.
15 Los pesos (en kg) de 24 personas son: 68,5 34,2 47,5 39,2 47,3 79,2 46,5 58,3 62,5 58,7 80 63,4 58,6 50,2 60,5 70,8 30,5 42,7 59,4 39,3 48,6 56,8 72 60
- Agrúpalos en intervalos de amplitud 10 y obtén la tabla de frecuencias.
- ¿Cuántas personas pesan menos de 50 kg?
- Calcula el tanto por ciento sobre el total que representa el intervalo de mayor frecuencia absoluta.
16 ¿Por qué los intervalos en las tablas son cerrados por un lado y abiertos por el otro?
17 Las estaturas (en cm) de 28 jóvenes son:
155 178 170 165 173 168 160 166 176 169 158 170 179 161 164 156 170 171 167 151 163 158 164 174 176 164 154 157
Forma una tabla con intervalos, efectúa el recuento y obtén las marcas de clase.
13 ¿Qué ocurre si la suma de las frecuencias absolutas no es igual al número total de datos?
Gráficos estadísticos
Diagrama de barras
21 En un edificio de 16 vecinos, el número de televisores por vivienda es:
0, 1, 1, 2, 1, 3, 2, 1, 1, 1, 2, 2, 3, 0, 3, 2
- Construye la tabla de frecuencias. ¿Qué tipo de variable es? Razona tu respuesta.
- Realiza el diagrama de barras y el polígono de frecuencias de los datos.
- Haz lo mismo con las frecuencias acumuladas.
22 En un aparcamiento público hay 25 coches rojos, 19 amarillos, 39 plateados, 50 blancos, 27 verdes, 30 azules y 10 negros.
- Construye la tabla de frecuencias.
- ¿Puedes hallar las frecuencias acumuladas?
- Realiza el diagrama de barras.
23 Haz los gráficos del ejercicio anterior con las frecuencias relativas. ¿Qué observas?
Histograma y polígono de frecuencias
26 La longitud (en cm) de 18 grillos es:
1.8, 1.9, 2, 2.4, 2.6, 2.8, 1.7, 1.9, 2.3, 1.6, 2.1, 3, 2.3, 2.7, 2.9, 1.5, 1.8, 2.6
- Construye la tabla de frecuencias tomando intervalos.
- Representa los datos mediante un histograma y un polígono de frecuencias.
Diagrama de sectores
27 El peso (en kg) de 20 mochilas de estudiantes es: 4,2 – 3,8 – 5,1 – 4,5 – 3,9 – 4,7 – 5,3 – 4,8 – 4,1 – 5,0 3,7 – 4,6 – 5,2 – 4,3 – 4,9 – 3,6 – 5,4 – 4,0 – 4,4 – 3,5
- Construye la tabla de frecuencias tomando intervalos.
- Representa los datos mediante un histograma y un polígono de frecuencias.
- Realiza un diagrama de sectores.
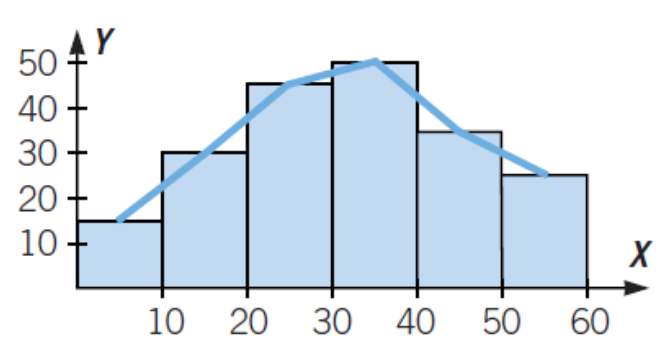
30 Haz la tabla de frecuencias que corresponde a este histograma.
Medidas estadísticas: medidas de posición
Las medidas de posición proporcionan información resumida de la variable objeto de estudio
Medidas de posición central: media, mediana y moda
Las medidas de centralización nos ayudan a resumir un conjunto de datos en un solo valor que represente el centro o la tendencia central de los datos.
Media
La media aritmética es el valor promedio de un conjunto de datos. Se calcula sumando todos los valores y dividiendo entre el número total de valores. La fórmula es:
\(\overline{x} = \frac{\sum_{i=1}^{n} x_i \cdot f_i}{n}\)
Mediana
La mediana es el valor que deja el mismo número de datos por encima y por debajo de él cuando los datos están ordenados.
Si hay un número impar de datos, la mediana es el valor central. Si hay un número par de datos, la mediana es la media de los dos valores centrales.
Moda
La moda es el valor que más se repite en un conjunto de datos.
Es posible que un conjunto de datos tenga más de una moda (si varios valores se repiten el mismo número de veces) o que no tenga moda (si ningún valor se repite).
32 Calcula la media, la mediana y la moda del número de suspensos de 15 alumnos. Interpreta el resultado:
4, 1, 0, 4, 1, 4, 1, 2, 3, 0, 2, 4, 0, 3, 1
35 Las estaturas (en cm) de 24 alumnos de 3.° ESO son:
158, 160, 168, 156, 166, 158, 160, 168, 168, 158, 156, 164, 162, 166, 164, 168, 162, 158, 156, 166, 160, 168, 160, 160
- Agrúpalas en intervalos.
- Realiza la tabla de frecuencias
- Calcula la media, mediana y moda.
36 Añade un valor que no haga variar la mediana.
18, 8, 7, 9, 12, 15, 21, 12
Medidas de posición no central: cuartiles
37 Calcula los cuartiles de este conjunto de datos que expresan los días de baja laboral sufridos por 10 trabajadores.
0, 2, 3, 4, 2, 1, 1, 0, 0, 3
38 Se han convocado unas oposiciones en las que hay 50 plazas y se han presentado 200 personas. Estos son los resultados:
| Notas | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|
| Opositores fi | 6 | 25 | 34 | 42 | 50 | 24 | 13 | 6 |
- Completa la tabla de frecuencias
- Calcula la media, mediana y moda.
- Calcula el primer cuartil.
- ¿Con qué nota se consigue una plaza?
Medidas estadísticas: medidas de dispersión
Las medidas de dispersión estudian la separación existente entre los valores que toma la variable.
Medidas de dispersión absolutas: desviación típica y varianza
\( \sigma^2 = \frac{\sum_i (X_i - \overline{x}) \cdot f_i}{N} \)
41 Las longitudes (en mm) de una muestra de tornillos son las siguientes. Calcula sus medidas de dispersión utilizando las marcas de clase.
| Intervalo | [13, 14) | [14, 15) | [15, 16) | [16, 17) |
|---|---|---|---|---|
| \(f_i\) | 8 | 7 | 2 | 3 |
Medidas de dispersión relativas: Coeficiente de variación
Se trata de una medida adimensional y sin unidades que nos permite comparar la dispersión de dos variables.
\(C_v = \frac{\sigma}{|\overline{x}|}\)
40 La anotación de dos jugadores de baloncesto en los últimos cinco partidos ha sido:
- Jugador A: 12, 15, 14, 13 y 16.
- Jugador B: 10, 18, 11, 17 y 15.
- Calcula la media y la varianza en los dos casos.
- Calcula su coeficiente de variación. ¿En cuál de los dos jugadores hay mayor dispersión?
42 Las notas obtenidas por un alumno en cinco exámenes han sido: 3, 8, 5, 7 y 4, y las de otro alumno: 2, 9, 4, 5 y 7. Calcula su coeficiente de variación. ¿En qué alumno es mayor la dispersión?