Tema 2: Fracciones y números decimales
¿Cómo se llama el número de arriba de las fracciones?
1
Numerador
2
Denominador
3
Resto
4
Cociente
... y el número de abajo?
1
Numerador
2
Denominador
3
Resto
4
Cociente
1 Indica si las siguientes fracciones son propias o impropias. Si son impropias, represéntalas como un número mixto:
- E \[ \frac{5}{3} \]
- a \[ \frac{2}{9} \]
- b \[ \frac{7}{2} \]
- c \[ \frac{8}{5} \]
Fracciones equivalentes
2 Indica cuatro fracciones equivalentes a las siguientes, dos por ampliación y dos por simplificación:
- a \[ \frac{8}{24} \]
- b \[ \frac{9}{18} \]
- c \[ \frac{4}{12} \]
3 Calcula la fracción equivalente irreducible de:
- E \[ \frac{14}{21} \]
- a \[ \frac{48}{32} \]
- b \[ \frac{75}{60} \]
- c \[ \frac{165}{99} \]
Calcular fracciones equivalentes con denominador común
4 Ordena los siguientes conjuntos de fracciones:
- a \[ \frac{3}{4}, \frac{2}{3}, \frac{1}{6} \]
- a \[ \frac{1}{2}, \frac{3}{5}, \frac{4}{7} \]
- b \[ \frac{3}{4}, \frac{2}{3}, \frac{1}{5}, \frac{4}{7}, \frac{5}{6}, 1 \]
- c \[ \frac{2}{5}, \frac{7}{10}, \frac{5}{9}, \frac{4}{9}, \frac{10}{18} \]
Suma y resta de fracciones
5 Realiza las siguientes sumas y restas de fracciones. Simplifica el resultado si es posible:
- a \[ \frac{3}{4} + \frac{2}{4} \]
- a \[ \frac{3}{4} + \frac{1}{2} \]
- b \[ \frac{3}{4} + \frac{1}{5} \]
- c \[ \frac{3}{4} - \frac{1}{5} \]
5 Realiza las siguientes sumas y restas de fracciones. Simplifica el resultado si es posible (cont.):
- d \[\frac{3}{4} + \frac{1}{5} + \frac{2}{3} \]
- e \[ \frac{3}{4} - \frac{1}{5} - \frac{2}{3} \]
- f \[ \frac{3}{4} + \frac{1}{5} + \frac{2}{3} + \frac{5}{12} \]
- g \[ \frac{3}{4} - \frac{1}{5} + \frac{5}{6} - \frac{8}{10} \]
Multiplicación y división de fracciones
6 Opera:
- a \[ \frac{2}{3} \cdot \frac{4}{5} \]
- b \[ \frac{5}{7} \cdot \frac{2}{5} \]
- c \[ \frac{3}{6} \cdot \frac{2}{5} \]
- d \[ \frac{1}{2} \cdot \frac{3}{5} \cdot \frac{5}{2} \]
6 Opera (cont.):
- e \[ \frac{2}{3} : \frac{4}{5} \]
- f \[ \frac{5}{7} : \frac{2}{5} \]
- g \[ \frac{3}{6} : \frac{2}{5} \]
- h \[ \frac{1}{2} : \frac{3}{5} \]
Operaciones combinadas con fracciones
7 Calcula y simplifica el resultado:
- a \[ \frac{1}{2} \cdot (\frac{3}{2} + \frac{2}{3}) \]
- b \[ \frac{1}{2} \cdot \frac{3}{2} + \frac{2}{3} \]
- c \[ \frac{1}{2} + \frac{3}{2} \cdot \frac{14}{5} \]
- d \[ \frac{2}{5} \cdot \frac{1}{2} + \frac{4}{3} - \frac{1}{6} \]
7 Calcula y simplifica el resultado (cont.):
- e \[ \frac{2}{5} + \frac{1}{2} \cdot \frac{4}{3} - \frac{1}{6} \]
- f \[ \frac{3}{2} - \frac{4}{5} \cdot \frac{5}{6} \]
- g \[ (\frac{3}{2} - \frac{4}{5}) \cdot \frac{5}{6} \]
- h \[ \frac{7}{2} + \frac{1}{5} \cdot \frac{5}{6} \]
7 Calcula y simplifica el resultado (cont.):
- i \[ \frac{5}{3} : \frac{1}{9} + \frac{1}{6} \]
- j \[ -\frac{4}{7} + \frac{12}{5} - \frac{3}{4} \cdot (-\frac{5}{6}) \]
- k \[ -\frac{4}{7} + (\frac{12}{5} - \frac{3}{4}) \cdot (-\frac{5}{6}) \]
- l \[ \frac{4}{7} + (-\frac{12}{5}): (-\frac{4}{4}) \]
Números decimales
8 Ordena los siguientes número decimales:
- a 0.2, 1.123, 0.123, 1.2
- b 2.3, 1.25, -0.8, 0.5, -0.15
- c 0.5, 0.48, -0.345, 0.456
9 Realiza las siguientes sumas y restas de números decimales:
- a \[ 0.234 + 23.12 \] \[ = 23.354 \]
- b \[ 12.812 + 1.00234 \] \[ = 13.81434 \]
- c \[ 13.123 - 4.54 \] \[ = 8.583 \]
10 Realiza las siguientes multiplicaciones y divisiones de números decimales:
- a \[ 123.12 \cdot 2.3 \] \[ = 283.176 \]
- b \[ 234.45 : 1.2 \] \[ = 195.35 \]
- c \[ 127.28 \cdot 1.7 \]
- d \[ 284 : 0.3 \]
- e \[ 0.37 : 8 \]
- f \[ 3.28 \cdot 8 \]
Luns, 4 de noviembre
R1 Opera:
- a \[ \frac{2}{3} - (2 \cdot \frac{4}{5} + \frac{1}{5}) \]
- b \[ \frac{1}{2} - \frac{5}{2} \cdot (\frac{1}{3} - \frac{4}{5}) \]
Paso de fraccion a decimal
11 Pasa las siguientes fracciones a número decimal:
- a \[ \frac{1}{9} \]
- b \[ \frac{1}{2} \]
- c \[ \frac{3}{11} \]
12 Pasa las fracciones a decimal y opera:
- a \[ \frac{2}{3} - (2 \cdot \frac{4}{5} + \frac{1}{5}) \]
- b \[ \frac{1}{2} - \frac{5}{2} \cdot (\frac{1}{3} - \frac{4}{5}) \]
Martes, 5 de noviembre
13 Realiza las siguientes operaciones combinadas con números decimales:
- a \[ -3.14 \cdot (-2 + 1.8 \cdot 3.9) \]
- b \[ (-0.94 + 3.91) : 8.51 \]
- c \[ 28.36 - 5.2 \cdot 4.02 \]
Míercoles, 6 de noviembre
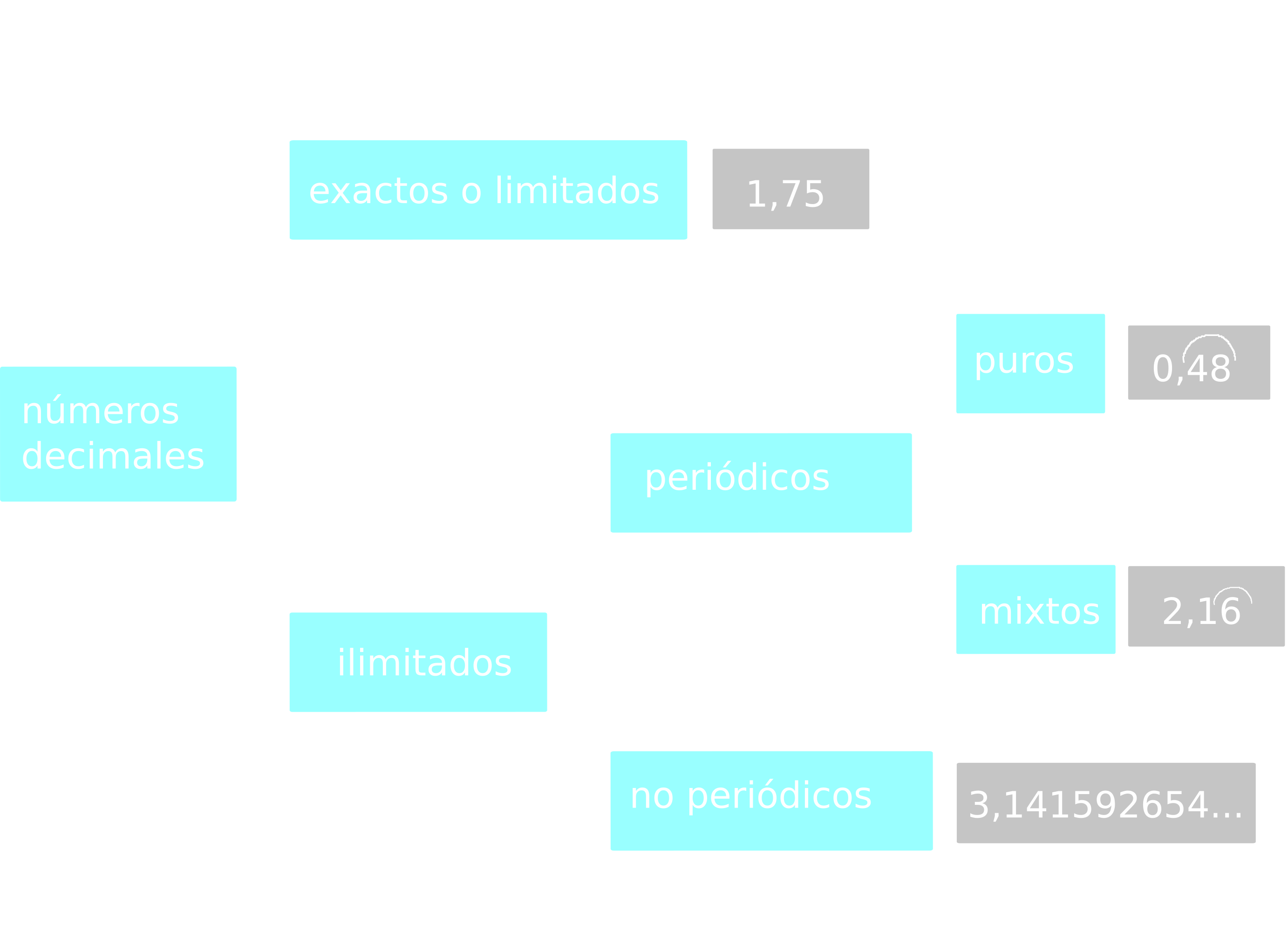
14 Indica de que tipo son los siguientes números decimales:
- a \[ 3.1222222222222\dots \] Periódico mixto
- b \[ 0.13 \] Exacto
- c \[ 0.232323232323\dots \] Periódico puro
- d \[ 0.2144444444444\dots \] Periódico mixto
Paso de decimal a fracción
15 Pasa los siguientes números decimales a fracción y simplifica donde sea posible:
- a \[ 3.4 \] \[ = \frac{34}{10} = \frac{17}{5} \]
- b \[ 2.52 \] \[ = \frac{252}{100} = \frac{36}{25} \]
- c \[ 0.125 \] \[ = \frac{125}{1000} = \frac{1}{8} \]
R2 Indica si las siguientes fracciones son propias o impropias. Convierte las impropias a número mixto:
- a \[ \frac{10}{9} \] \[ = 1 +\frac{1}{9} \]
- b \[ \frac{13}{20} \] (propia)
- c \[ \frac{10}{7} \] \[ = 1 +\frac{3}{7} \]
- d \[ \frac{5}{8} \] (propia)
Jueves y Viernes, 5 y 6 de noviembre
Paso de decimal a fracción
(periódicos)
16 Pasa los siguientes números decimales periódicos a fracción y simplifica donde sea posible:
- a \[ \]
- b \[ \]
- c \[ \]
- d \[ \]
17 Pasa los siguientes números decimales periódicos a fracción y simplifica donde sea posible (usa la demostración de la fórmula):
- a \[ \]
- b \[ \]
- c \[ \]
- d \[ \]
Lunes y martes, 11 y 12 de noviembre
Problemas
Aproximación de números
10 Aproxima los siguientes números por redondeo y truncamiento:
- a \[ 9.876 \] (décimas)
- b \[ 0.973 \] (centésimas)
- c \[ 2.497 \] (unidades)
Errores absoluto y relativo
\[E_a = |V_{estimado} - V_{real}| \]
\[E_r = \frac{E_a}{V_{real}} = \frac{|V_{estimado} - V_{real}|}{V_{real}} \]
11 Calcula el error absoluto y relativo cometido:
- a Al aproximar \[ 9.876 \] con \[ 9.9 \]
- b Al aproximar \[ 9.876 \] con \[ 9.8 \]
- c Al aproximar \[ 9.973 \] con \[ 9.97 \]