Números Enteros
Números negativos
Números negativos
Los números negativos son aquellos que están por debajo de cero en la recta numérica. Representan cantidades como deudas o temperaturas bajo cero. Se denotan con el signo menos (-) delante del número.
Por ejemplo, una temperatura bajo cero podría ser -3º C.
1 Expresa estos enunciados con un número positivo, negativo o cero:
- El punto de fusión del hidrógeno es 259 grados bajo cero.
- La altitud con respecto al nivel del mar si estoy sitúado en la orilla de la playa.
- El Titanic está sumergido a 3800m bajo el nivel del mar.
- Saldo de mi cuenta bancaria si tengo ahorrados 2000€.
2 Indica el significado de los números negativos en cada una de las situaciones:
- -4: Temperatura
- -200: El balance de cuenta
- -50: Posición con respecto al nivel del mar de un submarino.
- -20: El año en el que ocurrió cierto suceso.
Valor absoluto
El valor absoluto de un número representa su distancia al cero en la recta numérica, independientemente de si es positivo o negativo.
Se denota por barras, por ejemplo, \( |−5| = 5 \).
3 Calcula el valor absoluto de los siguientes números:
- \(|−7|\)
- \(|4|\)
- \(|−12|\)
- \(|0|\)
Opuesto
El opuesto de un número es aquel que tiene el mismo valor numérico pero el signo contrario.
Por ejemplo, el opuesto de \(−3\) es \(3\), y el opuesto de \(4\) es \(−4\).
4 Calcula el opuesto de los siguientes números:
- \(Op(8)\)
- \(Op(-15)\)
- \(Op(7)\)
- \(Op(-3)\)
Representación en la recta numérica
Los números enteros pueden representarse en una recta numérica donde los valores a la derecha del cero son positivos y los de la izquierda son negativos.

5 Representa en la recta numérica los siguientes números:
- \(−3\)
- \(2\)
- \(0\)
- \(−5\)
6 Indica qué números están representados en la siguiente recta:
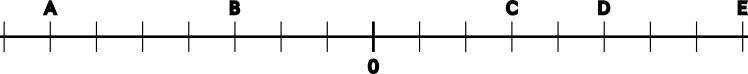
Comparación de números enteros
Para comparar números enteros, consideramos su posición en la recta numérica: los números más a la derecha son mayores, y los que están más a la izquierda son menores.
7 Ordena de menor a mayor las siguientes series de números enteros:
- \(-3, 0, 5, -1\)
- \(7, -8, 2, -4\)
- \(6, -2, 3, -5\)
- \(-6, 4, -1, 2\)
Operaciones con enteros
Suma y resta con resultados negativos
Al sumar o restar números enteros, si tienen el mismo signo, sumamos sus valores absolutos y mantenemos el signo. Si tienen signos opuestos, restamos el menor valor absoluto del mayor y usamos el signo del mayor.
8 Realiza las siguientes sumas y restas:
- \(7 − 3)\)
- \(−5 + 8\)
- \(−9 − 4)\)
- \(12 − 15\)
- \(2 + 7\)
- \(-5 + 3\)
Si tenemos más de números para restar y/o sumar, podemos:
- Hacer la operación de izquierda a derecha agrupando de 2 en dos.
Por ejemplo: \(-4 + 7 -2 + 5 = 3 - 2 +5 = 1 + 5 = 6 \) - Agrupar los números del mismo signo sumándo sus valores absolutos. Por ejemplo: \(-4 + 7 -2 + 5 = -6 + 12 = 6 \)<
9 Realiza las siguientes operaciones agrupando primero los números con el mismo signo:
- \(3 −7 + 5 - 4 + 3 + 2\)
- \(−4 + −6 + 8 - 2 - 4\)
- \(−10 + 12 − 5 + 3 + 1\)
- \(15 − 3 − 4 - 1 + 7\)
Regla de los signos
- \(1 + (+2) = 1 + 2 = 3 \)
- \(1 + (-2) = 1 - 2 = -1 \)
- \(1 - (+2) = 1 - 2 = -1 \)
- \(1 - (-2) = 1 + 2 = 3 \)
10 Realiza las siguientes sumas y restas aplicando la regla de los signos:
- \( ( +3) - ( -5)\)
- \( ( -2) + ( -3)\)
- \( ( +6) + (+10)\)
- \( (-10) + ( +5)\)
- \( (+13) - (+20) \)
11 Realiza las siguientes operaciones paso a paso:
- \( (-6) + (−2) − (+4) + (-8) \)
- \( (−7) + (+5) − (+3) - (+4)\)
- \( (+12) − (+9) + (−6) - (-3)\)
- \( (−8) + (+4) + (−5) + (-7)\)
Multiplicación y división de números negativos
Cuando multiplicamos o dividimos dos números con el mismo signo, el resultado es positivo. Si tienen signos opuestos, el resultado es negativo.
12 Calcula las siguientes multiplicaciones y divisiones de números enteros:
- \( (−3) \cdot (+4)\)
- \( (−5) \cdot (−2)\)
- \( (+15) : (−3)\)
- \((−16) : (+4)\)
13 Resuelve las siguientes operaciones:
- \((−6) \cdot (−3) : 2\)
- \(5 \cdot (−4) \cdot 8\)
- \(10 : (−2) \cdot (-5)\)
- \((−12) : (-3) : 2\)
Potencias de números enteros
Las potencias de números enteros siguen ciertas reglas. Si el exponente es par, el resultado siempre es positivo; si es impar, el resultado tiene el mismo signo que la base.
14 Indica el signo de las siguientes potencias:
- \((−3)^4\)
- \((−2)^3\)
- \(5^2\)
- \((−1)^5\)
Operaciones combinadas con enteros
Jerarquía de operaciones con enteros
Para resolver operaciones combinadas, es importante seguir la jerarquía de operaciones: primero se resuelven las potencias y raíces, luego multiplicaciones y divisiones, y finalmente sumas y restas.
15 Resuelve las siguientes operaciones combinadas con números enteros:
- $(-5) \cdot (+6) - 8 + 12$
- $15 \div 3 - 4 \cdot (-2)$
- $(-10) + \left[5 \cdot (-3) + 8 \cdot (-4)\right]$
- $\left[20 \div (-5) - 6 \cdot (-3)\right] + 2 \cdot (-7)$
- $\left[\left(3 \cdot (-4) + 5 \right) \cdot (-2)\right] + \left(10 \cdot (-3) + 15\right)$
15
- $(-8) + 3 \cdot (-2) - \left[6 \cdot (+4) - 5\right]$
- $\left[15 - (-3) \cdot 6\right] + 8 \div (-4) - 7$
- $\left\{10 + \left[(-6) \cdot (+5) + 12\right]\right\} \cdot (-2)$
- $\left[(-4) \cdot (-6) + 6\right] \div \left[9 - 3 \cdot (-2)\right] + (-7)$
- $\left\{\left[(-5) \cdot 4 - (-8)\right] + 3 \cdot (-2)\right\} \cdot (-3) + 12$